Chaos theory ஒழுங்கின்மை கோட்பாடு

அறிமுகம்

அனிமேஷன் திரைப்படங்கள் என்கிற போது வயது வேறுபாடு இல்லாமல் சிறியவர்கள் முதல் பெரியவர்கள் வரை அனைவருமே விரும்பிப்பார்ப்பது வழமை. அந்த வரிசையில் ICE AGE திரைப்பட வரிசை எல்லா தரப்பினரிடையிலும் நல்ல வரவேற்பை பெற்ற ஒரு படவரிசை. அத்திரைப்படத்தில் நம்மை அநேகம் சிரிக்கவைக்கும் ஒரு கதாபாத்திரம் ஸ்கேர்ட் எனும் வரலாற்றுக்கு முந்தைய காலத்து அணில். தமிழ்  சினிமாக்களில் வரும் காமெடியன் கதாப்பாத்திரங்கள் போல் வெறுமென சிரிப்புக்காக மாத்திரம் அமைக்கப்பட்ட கதாப்பாத்திரமென இது தெரிந்தாலும்கூட ICE AGE திரைப்படவரிசையின் ஒவ்வொரு கதைக்குமான தொடக்கப்புள்ளியும், முற்றுப்புள்ளியும் ஸ்கேர்ட் கதாபாத்திரத்தின் ஒரு சிறு செயலே என்பதை உற்று நோக்குவதன் மூலம் கணிக்கலாம். எந்தவொரு திரைப்படத்தை பார்க்கும் போதும் ஒரு பகுதி ரசிகர்களிடையே இந்த ஒரு மனோபாவம் இருக்கும் “இந்த சீன் மட்டும் இப்படி போயிருந்தா,கதையே வேற மாதிரி இருந்திருக்கும்”. ட்விஸ்டுகளாகவோ, ஆன்டி க்ளைமாக்ஸ்களாகவோ ஏதோ ஒரு காட்சி மொத்தமாக படமொன்றின் போக்கையே மாற்றி விடுகிறது. சமீபகாலமாக இவ்வாறான ஒரு விமர்சனம் அதிகளவான மார்வெல் ரசிகர்களிடம் உள்ளது. சென்ற ஆண்டு வெளியாகி பெரும் வரவேற்பை பெற்ற Avengers Infinity war திரைப்படத்தில் தி கிரேட் வில்லனான தானோஸை ஏறக்குறைய வீழ்த்திவிட்ட சந்தர்ப்பத்தில் ஸ்டார் லோர்ட் கதாபாத்திரம் வெளிப்படுத்திய சிறியதொரு உணர்ச்சி பெருக்கால், ஒட்டுமொத்த பிரபஞ்சத்தின் சரிபாதி உயிரினங்கள் அழிந்துவிட்டன. சிறியதொரு அவசரத்தில் விளைவை அந்த காட்சி மிகவும் ஆழமாக பதிவு செய்திருக்கிறது.

திரைப்படங்கள் என்கிற நிலையையும் தாண்டி நம்முடைய அன்றாட வாழ்கையிலும் இத்தகைய சொல்லாடல்கள் எழுவதுண்டு. “அன்னைக்கு ஒரு நாள் எனக்கு இந்த ஹெல்ப் கிடைச்சிருக்கலனா, இன்னைக்கு என்னால இந்த வாழ்கைய வாழ்ந்துட்டு இருக்க முடியாது” என்ற நன்றி நவிழ்தல்களும், “இத அப்போவே சொல்லியிருந்தா பிரச்சினை இவ்வளவு மோசமா போயிருக்குமா?” என கொட்டித்தீர்த்தது கொள்ளும் ஆதங்கங்களும் ஒன்றை நமக்கு அடிக்கடி உணர்த்திக்கொண்டே இருக்கின்றது. அது ஏதெனில், ‘நம்வாழ்வில் நாம் என்றோ, எங்கோ செய்துவிட்ட காரியத்தின் எச்சமொன்று காலங்களை தாண்டி எதிர்பாராத பொழுதொன்றில் நம்மையோ, நம்மை சார்ந்தவர்களையோ, வெளிநபர் ஒருவரையே ஏதோ ஒரு விதத்தில் தாக்குதல் கூடும்’. புரிந்துகொள்வதற்கு கடினமான இந்த ஒழுங்கின்மை பிரபஞ்சத்தின் எல்லா செயல்களையும் ஒன்றுடன் ஒன்று தொடர்புபடுத்துகிறது. சிலந்திவலையை போன்றதொரு ஒழுங்கற்ற தொடர்புகளால் நாம் அனைவரும் ஒருவரோடு ஒருவர் பிணைக்கப்பட்டுள்ளோம். இத்தொடர்பை விளங்குவதற்கு முன்வைக்கப்பட்ட விஞ்ஞான பூர்வமான விளக்கமே குழப்பவாதம். குழப்பவாதம் எனும் சொல்லே அதனை புரிந்துகொள்வதில் உள்ள கடினத்தை நமக்கு வெளிச்சமிட்டு காட்டிவிடுகிறது. எனினும் வாசகர்கள் சற்றே பொறுமையுடன் வாசித்தால் நிச்சயமாக குழப்பவாதம் குறித்தான அடிப்படை எண்ணக்கருவை விளங்கிக்கொள்ளமுடியும்.

குழப்பவாதம் /ஒழுங்கின்மை கோட்பாடு : விளக்கம்

குழப்பவாதம் என்பது ஒழுங்கின்மையையும், எதிர்பாராத விளைவுகளையும் தன்னகத்தே கொண்டது. எதிர்பாராததை எதிர்பார்க்க கற்றுக்கொடுக்கும் ஒரு விஞ்ஞான வாதம். பெரும்பாலான பாரம்பரிய விஞ்ஞானங்கள் விளைவுகளை முன்னரே யூகிக்கக்கூடிய ஈர்ப்பு விசை, மின்சாரம் மற்றும் இரசாயன பரிசோதனைகள் போன்றவை குறித்து விளங்கங்களை தந்தவண்ணம் இருக்கையில் குழப்பவாதம் மாத்திரம் வானிலை, பங்குச்சந்தை மற்றும் மூளையில் ஏற்படும் உணர்ச்சி மாற்றங்கள் போன்ற அடிக்கடி மாற்றமடையும், முன்னறிவிப்பு செய்யமுடியாத விடயங்கள் பற்றிய ஆய்வுகளிலும், கணிப்புகளிலும் ஈடுபட்டுள்ள வண்ணம் காணப்படுகிறது. குழப்பங்களுக்கு என்றும் குறைவில்லாத கணிதத்துறையின் ஒரு விளக்கமே குழப்பவாதம் (ஒழுங்கின்மை வாதம்). இந்த நடத்தையானது சிக்கலான, அதீத உணர்திறன் மிக்க எந்தவொரு அமைப்பிலும் ஏற்படும்.அது கணினியாகவும் இருக்கலாம், சமூகமாகவும் இருக்கலாம். ஓர் சிறுமாற்றம் மொத்த தொகுதியையும் பாதிக்கும் வல்லமை கொண்டது. சிக்கலான வலையமைப்பை கொண்ட எந்தவொரு தொகுதியிலும் ஒரு சிறிய மாற்றமானது காலப்போக்கில் பாரிய வேறுபாட்டை உண்டுபண்ணும். இந்த காரணத்தால் தான் இத்துணை விஞ்ஞான வளர்ச்சியை அடைந்துவிட்ட பின்னரும் கூட, எதிர்வரும் ஒரு சிலநாட்களுக்கு மேலாக நம்மால் வானிலையை கணிக்க முடிவதில்லை. அதையும் மீறி மிகவும் துல்லியமான வானிலைத்தரவுகளை திரட்டிய பின்னர் கணிப்பீட்டை மேற்கொண்டாலும் கூட அதில் ஏற்படத்தக்க ஒருசிறிய மாற்றம் அனைத்து முயற்சியையும் பாழாக்கி விடும். எந்த ஒரு -சூப்பர் கம்ப்யூட்டராலும் கூட ஒரு சிறிய பட்டாம்பூச்சியின் படபடப்பு இந்த சூழலின் வானிலையில் ஏற்படுத்தக்கூடிய பாரிய மாற்றத்தை கணிக்கமுடியாது. இதுவே குழப்பவாத கோட்பாட்டில் மிகப்பிரபல்யம் மிக்க ‘பட்டாம்பூச்சி விளைவு’ (butterfly effect) எனப்படுகிறது.

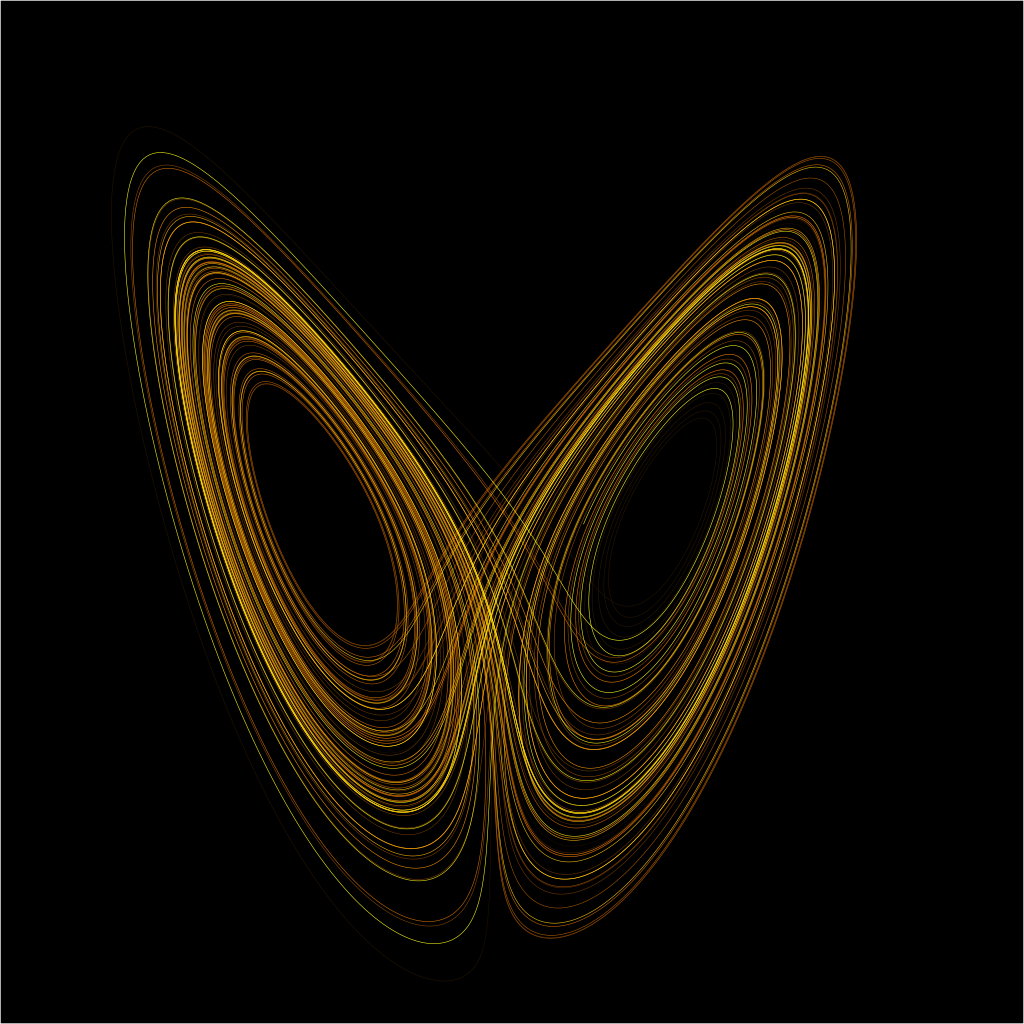
வானிலை உள்ளிட்ட அமைப்புகளை நாம் பார்க்கும் முதல் தடவையில் அவைகள் சீரற்றவையாக இருப்பதாக எண்ணக்கூடும், ஆனால் குழப்பவாதத்தை பொறுத்தவரையில் எந்தவொரு அமைப்பும் இவ்வாறு எழுந்தமானமாக மாற்றமடைய முடியாது. ஆனால் போதுமான அளவுக்கு பொறுமையை செலுத்தி கவனித்தால் அந்த அமைப்புகளில் ஏற்படும் யூகிக்கமுடியாத ஒரு ஒழுங்குமுறை இருப்பதை காணலாம். ‘முதல் கோணல் முற்றும் கோணல்’ என்பதே குழப்பவாதத்தின் அடிநாதம். அதாவது எந்தவொரு அமைப்பிலும், அதன் செயற்பாட்டின் ஆரம்பத்தில் உருவாகும் சிறுதவறு அந்த மொத்த அமைப்பின் செயலையும் பாதிக்கும்.

இதற்கான மிகச்சிறந்த ஒரு உதாரணம் கீழ்வருவது.

இணைக்கப்பட்ட இரு ஊசல் பலகைகளை மிகச்சிறிய இடைவெளியில் இருந்து தன்னிச்சையாக அலையவிடும் போது, இணைக்கப்பட்டுள்ள இரண்டாவது ஊசலானது முழுவதும் வித்தியாசமான, யூகிக்கமுடியாத ஒரு வழியில் தன்னுடைய அசைவை மேற்கொள்ளும். இரு ஊசல்களும் மீண்டும் ஒரே புள்ளியில் இருந்து தாமாக இயங்காது. ஆரம்பத்தில் உருவான மிகச்சிறிய வேறுபாடு ஒன்றினால் இந்த ஊசல்களின் மொத்த செயற்பாடும் அடியோடு மாறிவிட்டது. குழப்பவாதத்துடன் மிகவும் நெருங்கிய தொடர்பு உடைய கணித பாடப்பரப்பு பகுவல் (fractal) ஆகும். பகுவல் செயன்முறைகள் சிக்கலான ஒரு அமைப்பை கொண்டதே, குழப்பவாதத்தின் கோட்பாடுகளுக்கு அமைவாக பகுவல் செயன்முறையின் ஆரம்பத்தில் ஏற்படக்கூடிய ஒரு சிறிய தவறானது மொத்த விளைவுகளையும் மாற்றமடையச்செய்யும்.

குழப்பத்தின் தந்தை : எட்வர்ட் லாரன்ஸ்

குழப்பவாததிற்கு ஆதரவான கருத்தாக்கம் முதன்முதலில் 1880களில் ஹென்றி பொய்ன்க்ரே என்பவரால் முன்வைக்கப்பட்டது. எனினும் 1961 இல் வானியலாளரான எட்வர்ட் லாரன்ஸ் என்பவரே குழப்பவாதம் பற்றிய ஆழமான கண்டுபிடிப்பை உலகத்துக்கு தந்தார். லாரன்ஸ் புதிய கணினிகளை பயன்படுத்தி வானிலை முன்னறிவிப்புகளை துல்லியமாக முன்வைக்கும் பணியில் ஈடுபட்டிருந்தார். தற்போது சூழலில் நிலவும் வானிலை தரவுகளை உள்ளடக்கிய எண் தொகுதியை கணினியில் பதிவேற்றுவதன் மூலம் எதிர்வரும் சில நிமிடங்களுக்கான வானிலையை லாரன்ஸால் முன்னறிவிப்பு செய்யக்கூடியதாக இருந்தது. கணினி வழங்கிய வானிலை அறிக்கை சரியாக அமையத்தொடங்கியதும் தொடர்ச்சியாக நீண்ட காலத்துக்கான வானிலை முன்னறிவிப்பை மேற்கொள்வது குறித்து லாரன்ஸ் நம்பிக்கை கொண்டார். இதற்காக லாரன்ஸ் முன்னறிவிப்பு செய்யப்பட்ட வானிலைக்குரிய எண் தொகுதியை மீண்டும் கணினியில் பதிவேற்றம் செய்து இன்னும் சில நிமிடங்களுக்கு பிறகு நிலவப்போகும் வானிலையை உய்த்தறிந்தார். இதே செயன்முறையை பலமுறைகள் தொடர்ந்து செய்துகொண்டே இருப்பதன் மூலம் வருங்காலத்தில் வரும் வானிலை மாற்றங்கள் குறித்து முன்னதாகவே அறிந்துகொள்ள முடியும் என எதிர்பார்த்தார் லாரன்ஸ். எதிர்வரும் சிலநிமிடங்களுக்கு என மட்டுப்பட்டிருந்த லாரன்ஸின் எதிர்வுகூறல் எதிர்வரும் சில நாட்கள்,
சில வாரங்கள் என மெல்ல மெல்ல வளர்ச்சியடைந்தது. நாட்கள் இங்ஙனமே சென்றவண்ணம் இருக்க ஒருநாள் லாரன்ஸ் தன்னுடைய கணிப்புகளை மறுபரிசீலனை செய்ய முடிவெடுத்தார். நேரவிரயத்தை கவனத்தில் கொண்டு புதிதாக ஒரு கணிப்பை மேற்கொள்ள விரும்பாது, ஏற்கனவே செயற்பட்ட வண்ணம் இருந்த கணினி ஒன்றின் கணிப்பை எடுத்து அதனை புதிய கணிப்பின் ஆரம்பப்புள்ளியாக பயன்படுத்தினார். கணினியின் கணிப்புகளுக்கு போதுமான அவகாசத்தை வழங்கிவிட்டு, தானும் ஒரு காஃபி பிரேக்கை எடுத்துக்கொண்டு வேலைக்கு திரும்பிய லாரன்ஸ் ஒரு எதிர்பாராத விடயத்தைகண்டறிந்தார்.

கணினியின் புதிய கணிப்புகள் முந்தையதை போலவே இருந்தாலும் கூட, பின்னர் உருவான இரண்டு கணிப்புகள் மிகவும் வேகமாக அதிகளவு மாற்றமடையத்தொடங்கியது.
‘கணிப்பீட்டில் என்ன பிழைத்தது?’ என்று லாரன்ஸ் குழப்பமடைந்தார். கூடிய விரைவிலேயே அதற்கான காரணமும் லாரன்ஸின் கண்களுக்கு சிக்கின. ஆறு தசமதானங்களில் அச்சிடப்படவேண்டிய எண் கணிப்புகள், மூன்று தசமதானங்களுக்கு கணினியால் மட்டம் தட்டப்பட்டு இருந்தது. அதாவது இரண்டாவது பரிசோதனையில் 0.506 என்ற எண்ணை பயன்படுத்திய போது, உண்மையில் நடைபெற்ற முதல் பரிசோதனை அந்த எண் 0.506127 ஆக இருந்தது. இது ஆயிரத்தில் ஒரு பங்கு, எவ்வாறு பட்டாம்பூச்சியொன்றின் சிறகுகள் படபடத்து கொள்வது நம்முடைய முகத்தில் சிறியதாய் ஒரு காற்றோட்டத்தை உணரச்செய்கிறதோ அத்தகையதொரு சின்னஞ்சிறு வேறுபாடே இதுவும். ஆரம்பப்புள்ளிகள் இவ்வாறு மிகச்சிறிய வேறுப்பாட்டுடன் இருந்த போதிலும் கூட, அதை தொடர்ந்துவந்த கணிப்புகள் அவ்வாறு இருக்கவில்லை. இந்த சந்தர்ப்ப சூழ்நிலையே லாரன்ஸை குழப்பவாதத்தின் அடிப்படையை உணரச்செய்தது. குழப்பங்கள் எதுவுமின்றி நேர்த்தியாக செயல்படும் எந்தவொரு அமைப்பிலும் சிறியளவில் ஏற்படும் வேறுபாடுகள் சிறிய அளவு மாற்றத்தை மட்டுமே ஏற்படுத்தும் என லாரன்ஸ் தன்னுடைய முடிவை முன்வைத்தார். எனினும் காலப்போக்கில் லாரன்ஸின் சமன்பாடுகள் வளர்ச்சியடைந்து வந்த போது அதில் கணிசமான அளவு பிழைகள் உண்டாகின. அதாவது தற்போதைய காலநிலையை குறிக்க பயன்படும் எண் தொகுதியில் ஏற்படும் சிறியபிழை அச்சந்தர்பத்திற்கு வேண்டுமானால் சிறியதாக இருக்கலாம், ஆனால் அந்த பிழையான தரவை மீண்டும் மீண்டும் கணினியில் பதிவேற்றம் செய்து பெறப்படும் இறுதி முடிவானது மிகவும் பிழையானதாக இருக்கும் என்பது கண்டறியப்பட்டது. லாரன்ஸ் இந்த விளைவை மிகச்சிறப்பான ஒப்புவமையுடன் விளங்கப்படுத்தினார். அதுவே ‘பட்டாம்பூச்சி விளைவு’ (butterfly effect). எட்வர்ட் லாரன்ஸின் வானியல் ஆய்வே குழப்பவாதத்திற்கு உயிரளித்தது. சின்னஞ்சிறு மாற்றங்களே பாரிய விளைவுகளை தோற்றுவிக்கும் என்பதே குழப்பவாதத்தின் அடிப்படை.

குழப்பவாதத்திற்கான கோட்பாடுகள்

பட்டாம்பூச்சி விளைவு

குழப்பவாதத்தின் மிகப்பிரதான கோட்பாடு இந்த பட்டாம்பூச்சி விளைவு. பாரிஸ் நகரத்தில் ஒரு பட்டாம்பூச்சி தன்னுடைய சிறகுகளை படபடத்துக்கொள்வதன் விளைவாக அமெரிக்காவில் ஒரு ஹரிக்கேன் புயல் உருவாகக்கூடும். எல்லா ஹரிக்கேன் புயல்களுக்கும் பின்புலத்தில் ஒரு பட்டாம்பூச்சி இருப்பதாக நினைப்பது தவறு, அதே போல எல்லா பட்டாம்பூச்சியின் படபடப்பும் ஒரு புயலை உருவாக்குமெனில் தினமும் சூறாவளியாகதான் இருந்திருக்கும். எனவே தக்கதருணத்தில் சரியானதொரு இடத்தில் இருந்து ஏற்படும் ஒரு சிறிய பிழையே மொத்த விளைவையும் பாதிக்கும். ஆனால் அந்த சிறிய பிழை எது என்பது விளைவுகள் தோன்றிமறைந்த பின்னர்தான் கண்டறியப்படும். இந்த கணத்தில் நாம் செய்து கொண்டிருக்கும் இந்த ஐஐ செயலுமே வருங்காலத்தில் பாரிய விளைவை உண்டாக்கலாம். எனவே செய்யும் செயல் குறித்து விழிப்புடன் இருப்பது நலம்.

கணிக்கமுடியாத தன்மை

எந்தவொரு சிக்கலான அமைப்பினதும் ஆரம்பநிலை குறித்து 100% சரியான தரவுகளை நம்மால் பெறமுடியாது. இதனால் இந்த சிக்கலான அமைப்புகளின் எதிர்கால விளைவுகளையும் நம்மால் கணிக்க முடியாது. கணிப்புகளில் ஏற்படக்கூடிய எந்த ஒரு சிறுதவறும் மொத்த முடிவுகளிலும் பாரியமாற்றத்தை உண்டுபண்ணும். எனவே சிக்கலான அமைப்புகளை குறித்து நாம் கணிப்பது முற்றிலும் பயனற்றது. இன்றைய திகதியில் கூட உலகத்தில் எத்தனையோ பட்டாம்பூச்சிகள் சிறக்கடித்திருக்கும். ஆனால் அதனால் பின்னாட்களில் ஏற்படப்போகும் விளைவை இப்போது நம்மால் கணிக்கவே முடியாது.

கலப்பு

குழப்பவாதத்தின் படி, சிக்கலான அமைப்பொன்றில் அருகருகே இருக்கும் இரு புள்ளிகள் கூட ஒன்றில் இருந்து ஒன்று மிகவும் தொலைவாக செல்லும் என்பதை கூறுகிறது. உதாரணமாக ஒரு தொகுதி ஹீலியம் பலூன்களை விண்ணில் பறக்கவிடும் போது, அவை ஒவ்வொன்றும் சிறிது நேரத்திற்கு பிறகு வெவ்வேறு திசைகளில் பயணிக்க ஆரம்பித்து விடும். அவை வெடித்து நிலம்படும் இடங்களும் ஒன்றிலிருந்து ஒன்று வேறுபட்டே இருக்கும். கலப்பு என்பது எப்போதும் முழுமையானதே, காரணம் எல்லா சிக்கலான அமைப்பிலும் ஏதேனும் ஒரு வகையில் இருகொந்தளிப்பு ஏற்படும். அந்த கொந்தளிப்பு இவ்வாறான கலப்பை உறுதிசெய்யும்.

பின்னூட்டம்

பின்னூட்டங்கள்(feedbacks) இருக்கும் தருணங்களில் பெரும்பாலும் எந்தவொரு அமைப்பும் குழப்பமானதாகிவிடும். இதனை பங்குச்சந்தை நடத்தையில் தெளிவாக காணலாம். பங்குகளின் விலைகள் அதிகரித்தாலோ அல்லது குறைந்தாலோ அதற்கு ஏற்றவண்ணம் மக்கள் பங்குகளை கொள்வனவு செய்யவோ, அல்லது விற்பனை செய்யவோ முன்வருவார்கள். மக்களின் இந்த நடத்தை பங்குகளின் விலைகளில் மேலுமொரு குழப்பகரமான விலைமாற்றத்தை ஏற்படுத்தும்.

பகுவம்

பகுவம்(fractal) எனப்படுவது முடிவில்லா மாதிரி. இவை வெவ்வேறு அளவுகளில் ஒன்றையொன்று ஒத்ததாக இருக்கும் சிக்கலான வடிவங்களின் தொகுப்பு. ஒரு எளிமையான செயன்முறையை மீண்டும் மீண்டும் தொடர்ந்து செய்யும் ஒரு பின்னூட்டல் செயற்பாட்டாலேயே பகுவத்தின் வடிவங்கள் உருவாக்கப்படுகின்றன. பகுவங்கள் என்பது இயக்கமுறைகளின் படங்கள், இவையே குழப்பவாதத்தை வெளிப்படுத்த பயன்படுத்தப்படுகிறது. கணிதரீதியாக பகுவங்கள் நமக்கு பரிச்சயமான பரிமாணங்களிடையே அதிகளவில் காணப்படுகிறது.
நதிகள், மரங்கள், புயல்களென நம்மைச்சுற்றி இயற்கையின் மாறுபடும் அம்சங்கள்
நிறைந்திருக்கும் வரையில் குழப்பவாதம் விலக்கப்பட்ட வண்ணமே இருக்கும்.

முடிவாக…

இன்றைய திகதியில் ஒரு பல்தேசிய கம்பெனியும், அரசியல் தலைமையும் தங்களின் நலனுக்காக எடுக்கும் முடிவுகள் பொதுஜனத்தின் கழுத்துக்களை நெறிப்பதும், அடக்குமுறைகளுக்கு எதிராக எங்கேயோ ஒரு மூலையில் எழுப்பப்படும் வலுவான எதிர்ப்புக்குரல் ஒட்டுமொத்த உலகத்தையும் புதியதொரு பாதைக்கு அழைத்துச்செல்வதும் மேற்சொன்ன குழப்பவாதத்தின் வெளிப்பாடுகளே. சிறியதொரு மரம் நடுவதின் பயன்கூட இப்போது நமக்கு தெரியாது போகலாம், ஆனால் காலத்தின் வேகத்தில் அவை நிச்சயமாக பெரும் அர்த்தத்தை வழங்கும். சிரியதோ அல்லது பெரியதோ அளவுகள் என்பது எப்போதும் முக்கியம் பெறுவதில்லை. சமூகத்திற்கு நலம் பயக்கும் விடயம் ஒன்று இருக்குமெனில் தயக்கமின்றி அச்செயலை செய்யலாம். இன்று இல்லாவிட்டாலும் என்றோ ஒருநாள் அவை உலகுக்கு நன்மை செய்யக்கூடும்.