
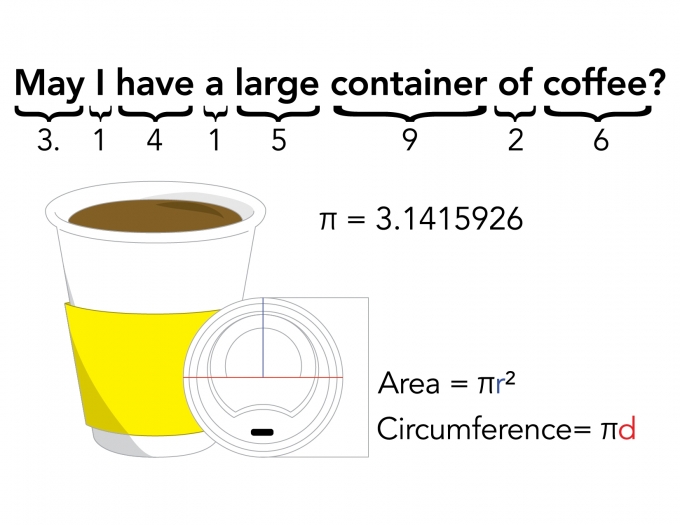
මාර්තු 14 හෙවත් 3/14 වෙන් කර ඇත්තේ ගණිත ලෝකයේ ජනප්රිය ම අපරිමේය සංඛ්යාවක් ලෙස සැලකිය හැකි ‘පයි’ නම් ගණිතමය නියතය සැමරීම සඳහා යි. ‘පයි’ හෝ π, වෘත්තයක පරිධිය සහ විෂ්කම්භය අතර අනුපාතය ලෙස සරල ව හැඳින්වීමේ වරදක් නැහැ. අපරිමේය සංඛ්යාවක් වන එහි අගය ලෙස සාමාන්යයෙන් භාවිතා කරන්නේ 3.14 යන අගය යි.
ගණිත විෂයය හැදෑරීම ඇරඹූ කාලයේ පටන් ම වෘත්තයක පරිධිය ගණනය කිරීම සඳහා යොදා ගත් ‘පයි’ භාවිතයට පැමිණියේ කෙසේ දැයි ඔබ දැන සිටියා ද? නොඑසේ නම් ඒ හා බැඳුණු අපූරු කරුණු පැවතිය හැකි බව ඔබ සිතා තිබුණා ද? මේ ලිපිය ගණිත ලෝකයේ අපරිමේය සගයා වන ‘පයි’ ගැන බොහෝ අය නොදන්නා අපූරු කරුණු කිහිපයක් ගැන යි.

© Pacific Standard
දශමස්ථාන 70,000 ක් කට පාඩමින්
අපරිමේය සංඛ්යාවක් වන ‘පයි’ සඳහා අවසානයක් නොමැති නමුත් විවිධ පුද්ගලයින් හැකිතාක් දුරට එය මතක තබා ගැනීම තුළින් වාර්තා පිහිටුවීමට උත්සාහ කර තිබෙනවා. දැනට ‘පයි’ හි දශමස්ථාන 70,000 ක් මතකයෙන් ඉදිරිපත් කිරීමට හිමි ගිනස් වාර්තාව හිමි කරගෙන ඇත්තේ ඉන්දියානු ජාතිකයෙක්. රාජ්වීර් මීනා නම් ඔහු එම වාර්තාව පිහිටුවා ඇත්තේ 2015 මාර්තු 21 වැනි දින යි. ඔහුට ඒ සඳහා පැය 10 ක කාලයක් ගත වී ඇති බව සඳහන්.
ඔහුට පෙර එම ගිනස් ලෝක වාර්තාව හිමිකම් කියන ලද්දේ 2005 වර්ෂයේ දී දශමස්ථාන 67,890 ක් කට පාඩමින් ඉදිරිපත් කළ ලූ චාඕ නම් චීන ජාතිකයා යි. නමුත් නිල නොවන වාර්තාවලට අනුව අකිරා හරගුචි නම් ජපන් ජාතිකයෙකු 2005 දී ‘පයි’ හි දශමස්ථාන 100,000 ක් ද මෑත කාලීන ව දශමස්ථාන 117,000 ක් ද මතකයෙන් ඉදිරිපත් කරන අයුරු වීඩියෝ ගත කර තිබෙනවා.
‘පයි’ වෙනුවෙන් භාෂාවක්
සංඛ්යාවක් වෙනුවෙන් භාෂාවක් නිර්මාණ කිරීම විශ්මයජනක කරුණක්. ‘පයි’ වෙනුවෙන් නිර්මාණය කර ඇති භාෂාව හඳුන්වන්නේ ‘පයිලිෂ්’ (Pilish) ලෙස යි. ඒ අනුව පයිලිෂ් බසින් වාක්ය ගැළපීමේ දී යොදා ගන්න වචනවල ඇති අක්ෂර ගණන, ‘පයි’ හි සංඛ්යා අනුපිළිවෙළට සමාන විය යුතු වෙනවා. 2010 වර්ෂයේ දී මයික් කීත් නම් ලේඛකයා විසින් ප්රකාශයට පත් කරන ලද ‘Not A Wake’ නම් ග්රන්ථය සම්පූර්ණයෙන් ම ලියා ඇත්තේ පයිලිෂ් බසින්.
ක්රමයෙන් දීර්ඝ වූ අපරිමේය සංඛ්යාව
අනාගතයේ කිසිම දිනෙක අපරිමේය සංඛ්යාවක් වන ‘පයි’ හි අවසානයක් දැකීමට නොහැකි බව පැහැදිලි කරුණක්. නමුත් එහි දශමස්ථාන ගණනය කිරීම අද දක්වා ම අඛණ්ඩ ව සිදු වෙනවා. ක්රිස්තු පූර්ව 2,000 දී පමණ බැබිලෝනියාවේ වැසියන් ‘පයි’ සඳහා ලබා දී ඇත්තේ 3⅛ යන අගය යි. පසු කාලීන ව 1665 දී ශ්රීමත් අයිසැක් නිවුටන් විසින් ‘පයි’ හි දශමස්ථාන 16 ක් ගණනය කරන ලද අතර 1719 වර්ෂය වන විට ප්රංශ ගණිතඥයෙකු වූ තෝමස් ෆොන්ටේ ඩි ලයිනි එය දශමස්ථාන 127 ක් දක්වා වැඩි දියුණු කළා.
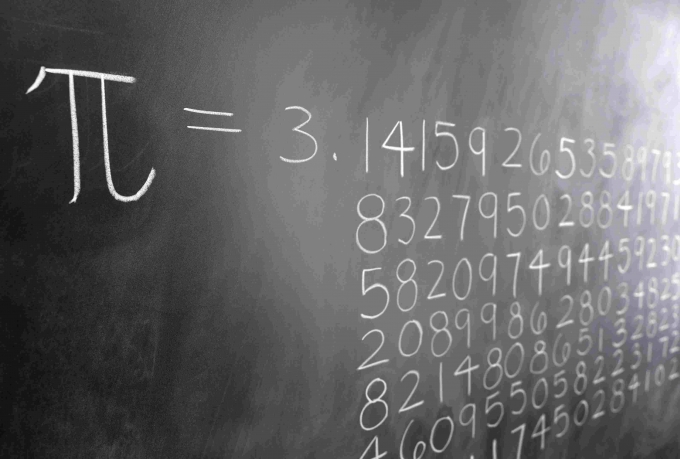
© Scientific American
පරිගණකයේ දියුණුව සමග ‘පයි’ හි දශමස්ථාන ගණනය කිරීම පහසු වූ අතර මේ වන විට ඩෙක්ට්රිස් නම් ස්විස් සමාගමට අනුබද්ධ ව සේවය කරන පීටර් ටෘෘබ් නම් විද්යාඥයා, පරිගණක මෘදුකාංගය සහය ඇති ව දින 105 කාල සීමාවක් තුළ දී ‘පයි’ හි දශමස්ථාන 22,459,157,718,361 ක් ගණනය කිරීමට සමත් වී ඇති බව සඳහන්.
වසර 4,000 ක් පැරණි ගණිත සගයා
පුරාවිද්යාත්මක සාක්ෂි පෙන්වා දෙන්නේ අදින් වසර 4,000 කට පමණ පෙර සිටි ම පුරාණ බැබිලෝනියාවේ වැසියන් ‘පයි’ නම් අපරිමේය සංඛ්යාව පිළිබඳ ව දැන සිටි බව යි. ක්රිස්තු පූර්ව 1900 – 1680 කාලයට අයත් බැබිලෝනියානු මැටි පුවරුවක ‘පයි’ හි අගය 3.125 ලෙස ගණනය කර ඇති අතර ඊජිප්තු ශිෂ්ටාචාරයට අයත් ක්රිස්තු පූර්ව 1650 දී සකසන ලද පැපිරස් පත්රයක ‘පයි’ හි අගය 3.1605 ලෙස දක්වා තිබෙනවා.

නමුත් ‘පයි’ හි අගය ප්රථම වරට නිවැරදි ව ගණනය කර ඇත්තේ ග්රීක ගණිතඥයෙකු වූ ආකිමීඩිස් විසින්. ඔහු ඒ සඳහා උපකාරී කරගෙන ඇත්තේ පයිතගරස් න්යාය යි. ඒ අනුව ‘පයි’ හි අගය 3⅐ ලෙස ඔප්පු කර පෙන්වීමට ඔහු සමත් වුණා.
‘පයි’ වෙනුවෙන් සංකේතයක්

© BBC
‘පයි’ වෙනුවෙන් යොදා ගන්නා ග්රීක සංකේතය භාවිතයට පැමිණීමට පෙර එය සංඛ්යාවක් ලෙස පැහැදිලි කිරීම සඳහා ගණිතඥයින්ට දීර්ඝ දේශනාවන් කිරීමට සිදු වී තිබෙනවා. මේ නිසා ඒ වෙනුවට සංකේතයක් හඳුන්වා දීමේ අවශ්යතාව මතු වුණා. ‘පයි’ සඳහා යොදා ගන්නා ලද ග්රීක අක්ෂරය වන π වඩාත් ප්රකට වුණේ 1737 දී ස්විස් බහුශාස්ත්රඥයෙකු වූ ලියන්හාර්ඩ් ඔයිලර් විසින් ප්රකාශයට පත් කරන ලද ත්රිකෝණමිතිය සඳහා වන නිබන්ධනය හේතුවෙන් වුව ද එය මුල් වරට භාවිතා කර ඇත්තේ විලියම් ජෝන්ස් නම් ගණිතඥයා යි. ඒ 1706 දී ප්රකාශයට පත් කරන ලද ඔහුගේ ‘Synopsis Palmariorum Matheseos’ නම් ග්රන්ථයේ දී යි.
3.14 සැමරීම සඳහා මාර්තු 14

© University of New Orleans
ලොව පුරා ගණිතඥයින් සමරනු ලබන ‘පයි’ දිනය යෙදී ඇත්තේ මාර්තු 14 වැනි දිනට යි. 1988 වර්ෂයේ දී ලැරී ෂෝ නම් භෞතික විද්යාඥයා සැන් ෆ්රැන්සිස්කෝ නුවර විද්යා කෞතුකාගාරයක දී මිතුරන් වෙනුවන් සාදයක් සංවිධානය කර මුල් වරට ‘පයි’ දිනය සමරා තිබෙනවා. නමුත් 2009 වර්ෂය දක්වා ම එය ජාතික උත්සවයක් ලෙස නම් කරන ලද්දේ නැහැ. 2009 මාර්තු 12 වැනි දින ඇමෙරිකා එක්සත් ජනපද නියෝජිත මන්ත්රී මණ්ඩලය අංක. 224 දරණ යෝජනාව සම්මත කිරීම මගින් ‘පයි’ දිනය ජාතික උත්සවයක් ලෙස පිළි ගනු ලැබුවා.
කවරයේ පින්තූරය : © Kuaza








