ইনফিনিট হোটেল প্যারাডক্স

আপনাকে যদি কখনো এক থেকে তিন এর মধ্যে কতটি সংখ্যা আছে তা গুনতে বলা তাহলে আপনি কী উত্তর দিবেন? যদি বলেন তিনটি তাহলে কিন্তু আপনার উত্তর পুরোপুরি সঠিক হল না। কারণ সংখ্যারেখার দিকে তাকালে দেখা যাবে এক থেকে তিন এর মধ্যে আছে অসংখ্য সংখ্যা। এই অসংখ্য পরিমাণটাই হল অসীম। বিশ্বকবি রবীন্দ্রনাথ ঠাকুর হয়তো অসীমত্বের ব্যাপারটা খুব ভালো বুঝেছিলেন। আর তাই তো তিনি বলেছিলেন, “সীমার মাঝে, অসীম, তুমি বাজাও আপন সুর”। অসীম কোনো সংখ্যা না, এটা একটা পরিমাণ নির্দেশ করে। যেমন, বাস্তব সংখ্যার সেট অসীম, আমাদের মহাবিশ্ব অসীম। অসীমের ব্যাপারে নতুন করে কিছু বলার নেই। অন্যভাবে বলা যায়, মানুষ এখনো যে সীমায় পৌছাতে পারেনি তা-ই অসীম।

এই অসীমত্বকে কাজে লাগিয়ে জার্মান গণিতবিদ ডেভিড হিলবার্ট একটি প্যারাডক্স তৈরি করেন যা ইনফিনিট হোটেল প্যারাডক্স বা হিলবার্টের গ্র্যান্ড হোটেল প্যারাডক্স নামে পরিচিত। এটি একধরনের চিন্তন পরীক্ষা যা দিয়ে অসীমত্বের একটি অনির্দিষ্ট ধর্মকে তুলে ধরা হয়েছে। ১৯২৪ সালে অসীম সম্পর্কে (জার্মান ভাষায় Über das Unendliche) এক লেকচারে তিনি এই প্যারাডক্সটি তুলে ধরেন। পরবর্তীতে ১৯৪৭ সালে জর্জ গ্যামোর প্রকাশিত বই “ওয়ান টু থ্রি… ইনফিনিটি” বইটিতে এই প্যারাডক্সটি উল্লেখ করা হয় আর তারপর থেকেই এটি বেশ জনপ্রিয়তা পায়।

এবার কল্পনার চিন্তার পালা শুরু। কেন কল্পনা? কারণ আদতে আপনি কখনো অসীম সংখ্যক কক্ষের হোটেল দেখতে পাবেন না। তাই তার আগে মাথাটা পুরো পরিষ্কার করে নিন, কারণ এই প্যারাডক্স আপনাকে অসীম এক কল্পনায় ডুবিয়ে দিবে।

ডেভিড হিলবার্ট; Source: bbvaopenmind

হিলবার্টের প্যারাডক্স

প্রথমেই আপনাকে একজন হোটেল ম্যানেজারের বেশ ধারণ করতে হবে। বিশেষ সেই হোটেলটি অসীম সংখ্যক তলা বিশিষ্ট, যার প্রতিটিতে আছে অসীম সংখ্যক কক্ষ। শুনতে বেশ কিম্ভুতকিমাকার হলেও এই হোটেলটি অসীম সখ্যক মানুষ দ্বারা পূর্ণ থাকার পরও তাতে আরো মানুষের জায়গা দেয়া সম্ভব। কিন্তু কিভাবে? এর তো শেষ কক্ষটি কোনটি সেটা তো আপনার জানা নেই। তাহলে নতুন কারো জায়গা দেবেন কিভাবে?

ইনফিনিট হোটেল প্যারাডক্স; Source: Ted Ed

নতুন অতিথি একজন হলে

হঠাৎ এক রাতে একা একজন অতিথি আপনার হোটেলে এলো। কিন্তু হোটেল তো পূর্ণ অসীম সংখ্যক মানুষ দিয়ে, আবার এত রাতে আপনি তাকে ফিরিয়েও দিতে পারেন না। এখন যা করা যায় তা হল হোটেলে অবস্থানরত প্রতিটি মানুষ তাদের পরবর্তী কক্ষে চলে যাবে। যেমন ১ নং কক্ষের মানুষটি যাবে ২ নং কক্ষে, ২ নং এর জন যাবে ৩ নং এ, ৩ নং এর জন যাবে ৪ নং এ… এবং n তম কক্ষের জন যাবে n +1 তম কক্ষে। এভাবে তা অসীম পর্যন্ত চলবে। ফলাফল নতুন অতিথির জন্য ১ নং কক্ষটি ফাঁকা হল। কিন্তু অসীম + ১ = অসীমই রয়ে গেল। আপনি এই যাত্রায় বেঁচে গেলেন। এবং বুঝে এরপর থেকে যেকোনো পরিমাণ গণনাযোগ্য অতিথির জন্য কক্ষ ফাঁকা করতে হবে “n + অতিথির সংখ্যা” এই  সূত্রে। কিন্তু যদি অসীম সংখ্যক অতিথি আসে?

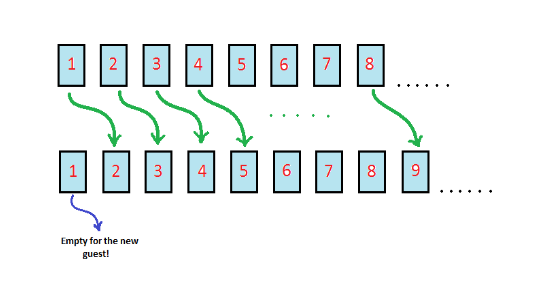
Source: intuitive science blog

নতুন অসীম সংখ্যক অতিথির আগমন

কোনো এক সকালে দেখলেন অসীম সংখ্যক যাত্রী নিয়ে একটা বাস হাজির এবং সকলেই অনেক গুরুত্বপূর্ণ ব্যক্তি। সুতরাং, এবারো আপনি কাউকে ফেরাতে পারছেন না। কিন্তু উপায়? উপায় আরো একটা আছে। বর্তমানে যে সকল অতিথি হোটেলে অবস্থান করছে তাদের দুটি দলে ভাগ করুন- জোড় এবং বিজোড়। n যদি তাদের বর্তমান কক্ষ নং হয় তাহলে তাদের 2n নং কক্ষে প্রতিস্থাপিত করুন। এর মাধ্যমে কিন্তু অসীম সংখ্যাক বিজোড় কক্ষ আপনি ফাঁকা করতে পারবেন। যেমন ১ নং কক্ষের অতিথি যাবে ২ নং এ, ২ নং এর জন যাবে ৪ নং এ, ৪ নং এর জন যাবে ৮ নং… 2n। আবার ৩ নং এর জন যাবে ৬ নং এ, ৬ নং এর জন যাবে ১২ নং এ, ১২ নং এর জন যাবে ২৪ নং এ… n তম কক্ষের অতিথি যাবে 2n তম কক্ষে। এখানে কিন্তু কখনোই বিজোড় তম কক্ষে বর্তমান অতিথিরা যাচ্ছেন না, যার ফলে অসীম সংখ্যক বিজোড় কক্ষ ফাঁকা হচ্ছে। এরপর আপনি ক্রমান্বয়ে আপনার গুরুত্বপূর্ণ অসীম সংখ্যক ব্যক্তিদের আপনার অসীম হোটেলে জায়গা দিতে পারবেন। কারণ অসীম + অসীম = অসীম।

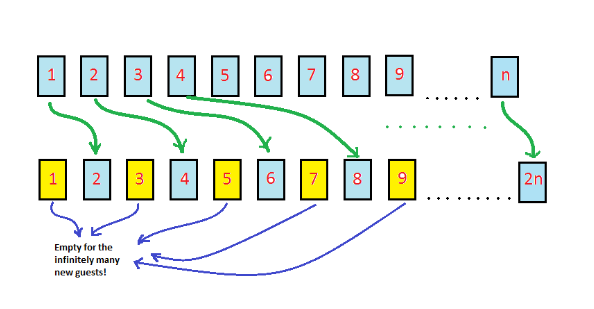
Source: intuitive science blog

অসীম সংখ্যক যাত্রী নিয়ে অসীম সংখ্যক বাস

গুরুত্বপূর্ণ সেই অতিথিদের জায়গা করে দিতে পারায় আপনার হোটেল ইতোমধ্যেই বেশ নাম কামিয়েছে। আর তার ফলাফল হঠাৎ একদিন অসীম সংখ্যক যাত্রীবাহী সেই বাস যার প্রত্যেকটি অসীম সংখ্যক যাত্রী বহন করে, আপনার হোটেলের সামনে হাজির। এবার তাদের জন্য জায়গা না দিলে আপনার হোটেলের অসীম পরিমাণ ক্ষতি হয়ে যাবে।

আপনার হয়ত সেই মুহূর্তে মাথা ঘোরাটা একটু স্বাভাবিক, কিন্তু একটু ভাবলেই এর সমাধান আপনি পেয়ে যাবেন। কারণ ইউক্লিড প্রমাণ করে গেছেন যে, মৌলিক সংখ্যার পরিমাণ অসীম। এবার এটাকে পুঁজি করে আমাদের সমস্যা সমাধানের পালা।

প্রথমেই হোটেলের বর্তমান অতিথিদেরকে সরাতে হবে প্রথম মৌলিক সংখ্যা ২ এর ঘাত অনুযায়ী। অর্থাৎ ২ নং কক্ষের অতিথি যাবে ২^২ = ৪ নং কক্ষে, ৩ নং কক্ষের অতিথি যাবেন ২^৩= ৮ নং কক্ষে… n তম কক্ষের অতিথি যাবেন ২^n  তম কক্ষে। দারুণ! অসীম পর্যন্ত কক্ষ ফাঁকা করা গেল। এর পরবর্তী কাজ হবে ১ম বাসের যাত্রীদের পরবর্তী মৌলিক সংখ্যা ৩ এর ঘাত অনুযায়ী হোটেলে জায়গা করে দেয়া। এবার ঘাত হবে ১ম বাসের যাত্রীদের আসন সংখ্যা। যেমন ১ম বাসের ৭ নং আসনের যাত্রী যাবে ৩^৭ = ২,১৮৭ নং কক্ষে।

Source: Ted Ed

এভাবে ১ম বাসের জন্য যাত্রীদের জন্য ৩ এর ঘাত, ২য় বাসের জন্য পরবর্তী মৌলিক সংখ্যা ৫ এর ঘাত, ৩য় বাসের জন্য ৭ এর ঘাত, ৪র্থ বাসের জন্য ১১ এর ঘাত… এভাবে অসীম সংখ্যক কক্ষের জন্য জায়গা দেয়া সম্ভব।

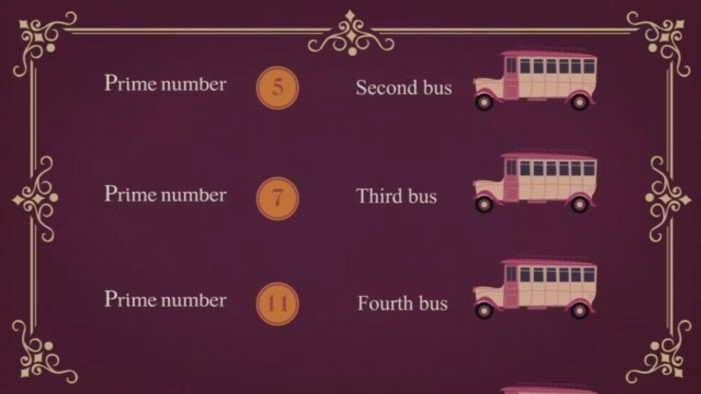
অসীম সংখ্যক যাত্রীদের মৌলিক সংখ্যার ঘাত অনুযায়ী জায়গা দেয়া; Source: Ted Ed

এই পদ্ধতি কাজ করবে, কারণ প্রতিটি কক্ষ প্রতিবারে ভিন্ন ভিন্ন পাওয়া যাবে এবং কোনো বারই তা একই রকম কক্ষকে অধিক্রমণ করবে না। কারণ এখানে বেজ সংখ্যাটি মৌলিক আর তাদের ঘাত স্বাভাবিক সংখ্যা। এখানে বেশ কিছু কক্ষ ফাঁকা থেকে যাবে, যেমন ৬, কারণ ৬ কোনো মৌলিক সংখ্যার ঘাতের ফলাফল না। কিন্তু এতে তেমন যায় আসে না।

এই পদ্ধতি কাজ করবে কেবলমাত্র গণনাযোগ্য অসীম স্বাভাবিক সংখ্যার ক্ষেত্রে, যেমন ১, ২, ৩ …। যদি অসীমের আরো গভীরে গিয়ে দশমিক বা ভগ্নাংশ আনা যেত তাহলে এভাবে সমস্যার সমাধান হতো না।

যাক, এই যাত্রাতেও বাঁচা গেল। ডেভিড হিলবার্টের এই প্যারাডক্সের আবির্ভাব হয়েছে আমাদের সসীম চিন্তাশক্তি দিয়ে অসীম ধরনের কোনো সমস্যা আমরা কিভাবে সমাধান করতে পারি তার জন্য।

কিন্তু অসীম পরিমাণ বেতন দিয়েও নিশ্চয় আপনি এই অসীম হোটেলের ম্যানেজার হতে চাইবেন না!