বিজ্ঞান বিভাগের ছাত্রদের শিক্ষাজীবনের প্রায় পুরোটাই নানারকম জটিল বিষয় শেখার মধ্য দিয়ে যেতে হয়। গণিত, পদার্থবিজ্ঞান, রসায়ন ইত্যাদি বিষয়ের একাধিক বই দিয়ে সচরাচর তাদের পড়ার টেবিল সাজানো থাকে। বোর্ড পরীক্ষায় ভালো করা, বিশ্ববিদ্যালয়ের ভর্তিযুদ্ধ- ইত্যাদি বিষয়কে কেন্দ্র করে রীতিমতো একটা সংগ্রাম চলতে থাকে। নানারকম গাণিতিক সূত্র, সমীকরণের সমাধান যেন তাদের দৈনন্দিন জীবনেরই একটা অংশ। আর একথা কেবল বিজ্ঞান বিভাগের শিক্ষার্থীদের জন্যই প্রযোজ্য নয়। অন্যান্য বিভাগের ছাত্রছাত্রীদেরও একই রকম ঝামেলা পোহাতে হয়।
এই যে আমরা আমাদের পুরো শিক্ষাজীবনে নানারকম গাণিতিক সমীকরণ শিখে আসছি, এগুলোর প্রয়োগ সম্পর্কে আমরা কতটুকুই বা জানি? পরীক্ষায় ভালো ফলাফল আনার মধ্যেই আমাদের কাছে এসব সমীকরণের প্রয়োজনীয়তা ফুরিয়ে যায়। কিন্তু এসব সমীকরণই যে আমাদের দৈনন্দিন জীবনকে একেবারে বদলে দিয়েছে, তা আমরা অনেকেই জানি না। আজ আমরা এই লেখাটিতে এমনই কিছু সমীকরণের বাস্তব প্রয়োগ সম্পর্কে জানব।
যারা নিজেদের গণিতে কাঁচা মনে করেন, তাদের ঘাবড়ে যাওয়ার কোনো কারণ নেই। এখানে কোনো জটিল সূত্রের ব্যাখ্যা করা হবে না। এসব ব্যাখার জন্য মোটা মোটা অনেক বই রয়েছে। এখানে কেবল এই সূত্রগুলো কীভাবে বাস্তব জীবনে কাজে লাগানো হয়, তা নিয়েই আলোচনা করা হবে।
পিথাগোরাসের সূত্র
উপপাদ্য ২৩-এর কথা মনে আছে? অষ্টম শ্রেণির সাধারণ গণিত পাঠ্যবইয়ে সব থেকে জনপ্রিয় ছিল এই উপপাদ্যটি। একটু জটিল হওয়ায় অনেক শিক্ষার্থীই এটিকে এড়িয়ে যেতে চায়। তবে গণিতের শাখায় এই সূত্রটি আসলে কতটা গুরুত্বপূর্ণ, তা বলে শেষ করা যাবে না।
সূত্রটির বিবৃতি মূলত এরকম,
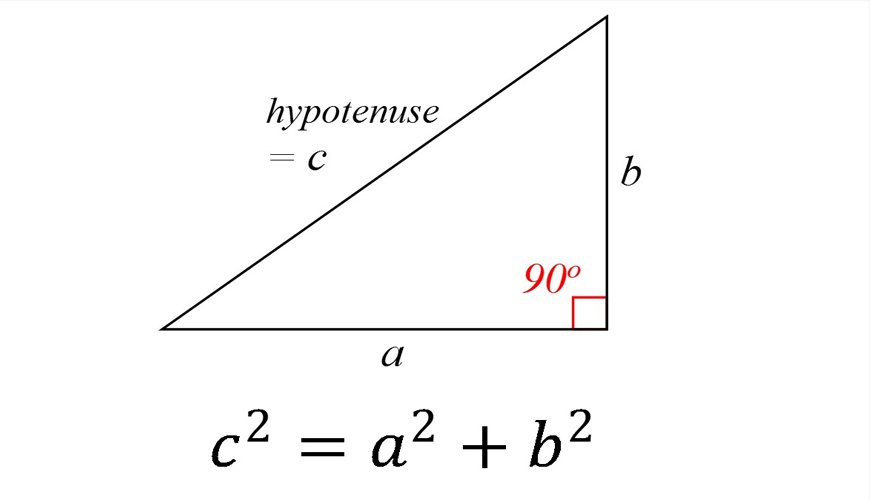
“একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল, এর ভূমি ও লম্বের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের যোগফলের সমান।
আমরা আপাতত এই সূত্রের ব্যাখায় যাব না। তবে পিথাগোরাসের এই সূত্রটি আসার পর থেকে ইউক্লিডীয় জ্যামিতির চিত্র বদলে যায়। আধুনিক মানচিত্রগুলোর নকশা করায় এই সূত্র ব্যবহার করা হয়ে থাকে। এছাড়াও দুটি বিন্দুর মাঝে ক্ষুদ্রতম দূরত্ব নির্ণয়, বসতবাড়ি তৈরির নকশা, কাঠের কাজ ইত্যাদিতে এই সূত্র ব্যাপকভাবে কাজে লাগে।
লগারিদম
কম্পিউটার আসার পর থেকে অনেক জটিল গাণিতিক হিসাব কয়েক মুহূর্তেই করে ফেলা সম্ভব। কিন্তু যখন কম্পিউটার ছিল না, তখনও বিজ্ঞানী ও গণিতবিদদের জটিল হিসাব করতে হতো। সেই সময় লগারিদম ছিল তাদের একমাত্র ভরসা। আজকের ক্যালকুলেটর তখনও আমাদের হাতে পৌঁছায়নি। জটিল হিসাব করার জন্য প্রকৌশলী ও গবেষকদের একটি লগারিদম টেবিলের সাহায্য নিতে হতো। লগারিদমের অনেক বড় সুবিধা হলো, এর মাধ্যমে জটিল গুণের কাজকে সহজে যোগের কাজে রূপান্তরিত করা যায়। তখনকার সময়ে এর সাহায্যে নানারকম জটিল গাণিতিক হিসাব করা সম্ভব হয়েছিল।
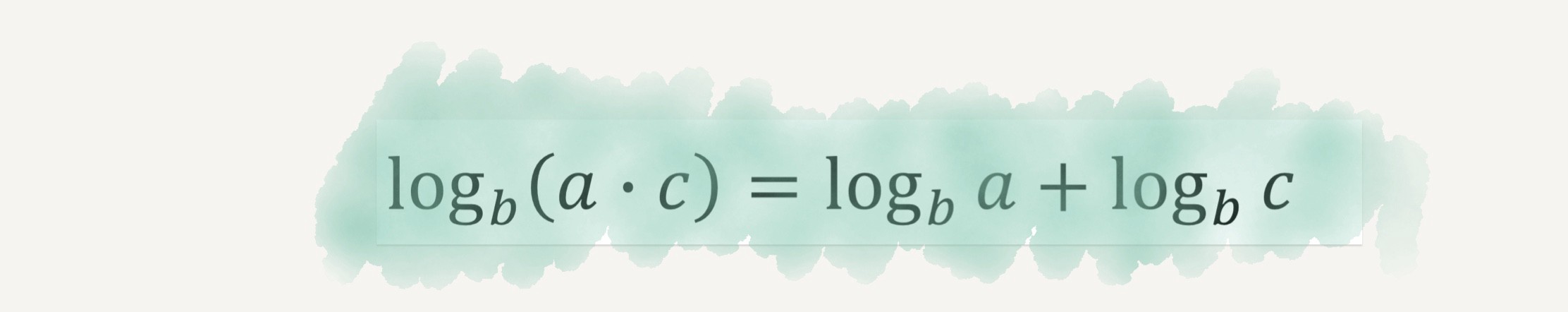

ক্যালকুলাস
আধুনিক বিজ্ঞানের পুরোটা জুড়েই রয়েছে ক্যালকুলাস। এই ক্যালকুলাস বলতে আসলে একটি বস্তুর সাপেক্ষে আরেকটি বস্তুর পরিবর্তনকে বোঝায়। এই যেমন সময়ের সাপেক্ষে দূরত্বের পরিবর্তন কিংবা সময়ের সাপেক্ষে তাপের পরিবর্তন ইত্যাদি। এই পরিবর্তন যখন খুবই ক্ষুদ্র পরিসরে হয়, তখনই আমরা ক্যালকুলাস ব্যবহার করে থাকি। মূলত বিজ্ঞানের কাজই হলো আমাদের চারপাশের পরিবর্তনগুলোকে পর্যবেক্ষণ করা।
শেয়ার বাজারের পণ্যের দরদাম, একটি রকেটকে মহাকাশে পাঠাতে কতটুকু জ্বালানি লাগবে, শরীরে ক্যান্সারের টিউমার কতদিন ধরে বৃদ্ধি পাচ্ছে- এসবের হিসাব করা যায় ক্যালকুলাসের সাহায্যে। মূলত আধুনিক বিজ্ঞান আজকের পর্যায়ে এসেছে এই ক্যালকুলাসের হাত ধরেই। অনেক গুরুত্বপূর্ণ গাণিতিক সমীকরণ রয়েছে, যেগুলো কেবল ক্যালকুলাসের মাধ্যমেই সমাধান করা যায়।
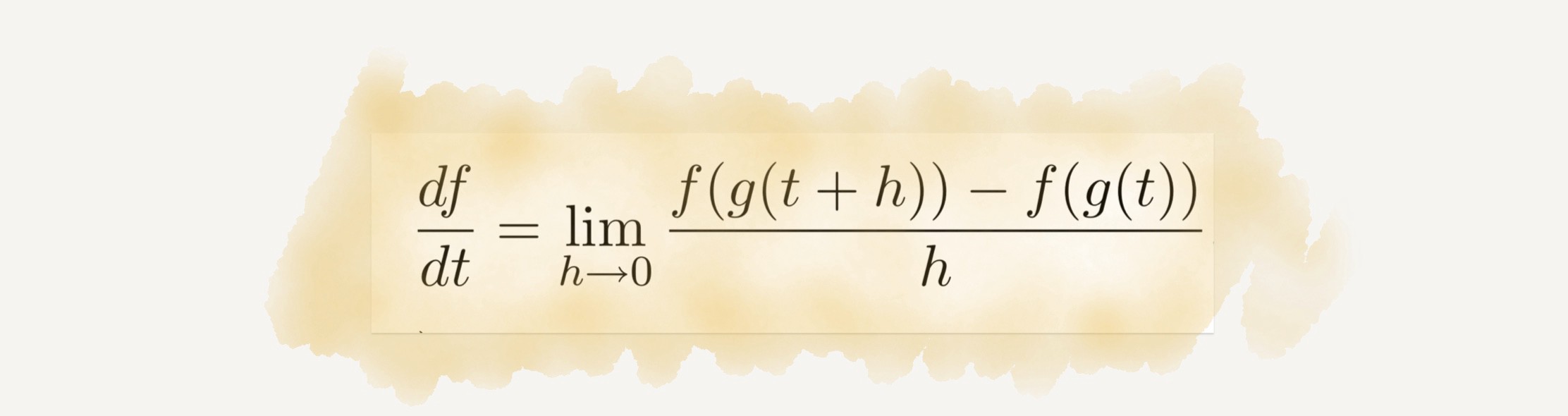
মহাকর্ষ সূত্র
বিজ্ঞানী স্যার আইজ্যাক নিউটন একদিন আপেল গাছের নিচে বসে গভীর চিন্তায় মগ্ন ছিলেন। হঠাৎ একটা আপেল তার মাথার উপর পড়ল। আর এখান থেকেই নিউটনের মাথায় প্রথম মহাকর্ষ শক্তি সম্পর্কে ধারণা আসে। এই কাহিনী কতটুকু সত্য, তা নিয়ে অনেক যুক্তিতর্ক থাকতে পারে। তবে নিউটনের মহাকর্ষ সূত্র যে পদার্থবিজ্ঞানের এক যুগান্তকারী আবিষ্কার, তাতে কোনো সন্দেহ নেই।
“মহাবিশ্বের যেকোনো দুইটি বস্তুকণার মাঝে একধরনের আকর্ষণ বল কাজ করে। এই আকর্ষণ বস্তু দু’টির ভরের গুণফলের সমানুপাতিক এবং এদের মধ্যবর্তী দূরত্বের বর্গের ব্যস্তানুপাতিক”
এটিই নিউটনের মহাকর্ষ সূত্র। এই সূত্রের সাহায্যে মহাকাশে গ্রহগুলো কেন একটি নির্দিষ্ট নক্ষত্রকে কেন্দ্র করে ঘুরছে, তার ব্যাখা দেওয়া যায়। প্রায় দুইশত বছর ধরে নিউটনের এই মহাকর্ষ সূত্র পদার্থবিজ্ঞানে এককভাবে রাজত্ব করেছিল। এরপর আইনস্টাইনের আপেক্ষিক তত্ত্বের আগমনের পর পদার্থবিজ্ঞানের এক নতুন দিগন্তের সূচনা হয়। তবুও একটি মৌলিক সূত্র হিসেবে এখনও মহাকর্ষ সূত্রের তাৎপর্য রয়েছে।
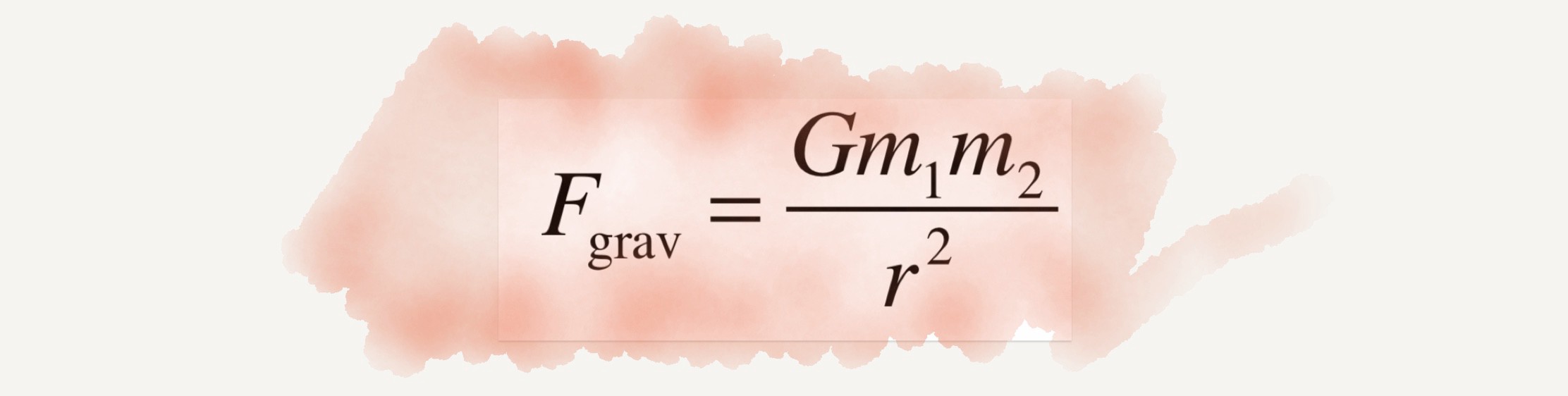
জটিল সংখ্যা
গণিতবিদরা একেবারে শুরু থেকেই সংখ্যা নিয়ে গবেষণা করে আসছেন। বাস্তব সংখ্যা, ধনাত্মক ও ঋণাত্মক সংখ্যা, ভগ্নাংশ ইত্যাদি নিয়ে তারা কাজ করেছেন। এরকম সংখ্যার প্রকারভেদের ভিড়ে নতুন যোগ করা হয়েছে জটিল সংখ্যা। এই জটিল সংখ্যা বলতে মূলত একটি ঋণাত্মক সংখ্যার বর্গমূলকে বোঝায়। নানা ধরণের জটিল সমীকরণের সমাধান বের করার সময় কিছু উত্তর ব্যাখা করা যেত না। জটিল সংখ্যার ধারণা আসার পর এগুলো জটিল বা অবাস্তব কোনো মান হিসেবে ব্যাখা করা যায়। মূলত ইলেকট্রনিক্স ও সিগনাল প্রসেসিংয়ের মতো বিষয়ে এই জটিল সংখ্যাগুলো বেশি কাজে লাগে।
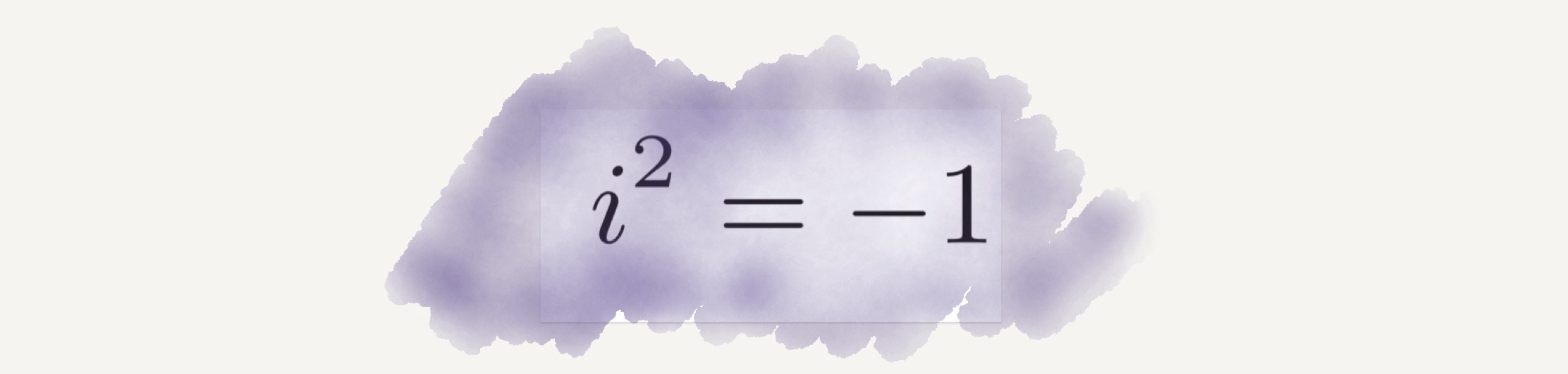
নরমাল ডিস্ট্রিবিউশন
পরিসংখ্যানের মতো বিষয়, অর্থাৎ যেখানে একই ধরনের অনেক তথ্য নিয়ে কাজ করা হয়, সেখানেই মূলত এই নরমাল ডিস্ট্রিবিউশনের সূত্র প্রয়োগ করা হয়। বিজ্ঞান, অর্থনীতি, এমনকি আমাদের দৈনন্দিন জীবনের সাথে সম্পর্কিত নানা ঘটনার সাথে নরমাল ডিস্ট্রিবিউশন জড়িয়ে আছে। কতগুলো তথ্যের মাঝে বিশেষ সম্পর্ক খুঁজে বের করার জন্য এই সূত্রটি প্রয়োগ করা হয়। সামগ্রিকভাবে একটি জনসংখ্যার উপর বের করা তত্ত্ব ও উপাত্ত বিশ্লেষণের কাজেই এই সূত্রটি কাজে লাগে।
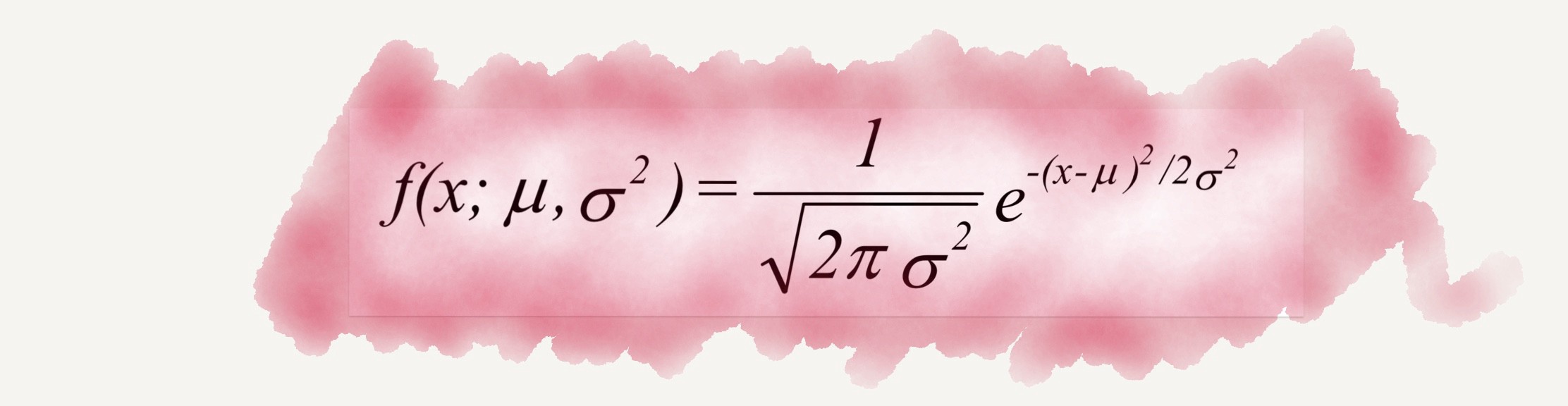
তরঙ্গ সমীকরণ
তরঙ্গের সমীকরণ বা ওয়েভ ইকুয়েশন দিয়ে আসলে তরঙ্গের আচরণ ব্যাখা করা হয়। এখানে তরঙ্গ বলতে কিন্তু শুধু পানির ঢেউয়ের কথা বোঝানো হয়নি। আমাদের চারপাশে বিভিন্ন ধরনের তরঙ্গ রয়েছে। তড়িৎচুম্বকীয় তরঙ্গ, আলোক তরঙ্গ ইত্যাদির অবস্থা বিশেষে পরিবর্তন এই সমীকরণ ব্যবহার করে পর্যবেক্ষণ করা হয়। পৃথিবীর প্রত্যেকটি পদার্থের নিজস্ব কম্পাঙ্ক রয়েছে। কাজেই এরা তরঙ্গ তৈরি করতে পারে। গিটারের তারের আওয়াজ হতে বৈদ্যুতিক বাল্বের আলো, মহাজাগতিক রশ্মি- সবকিছুই এই তরঙ্গ সমীকরণ দিয়ে ব্যাখা করা যায়।
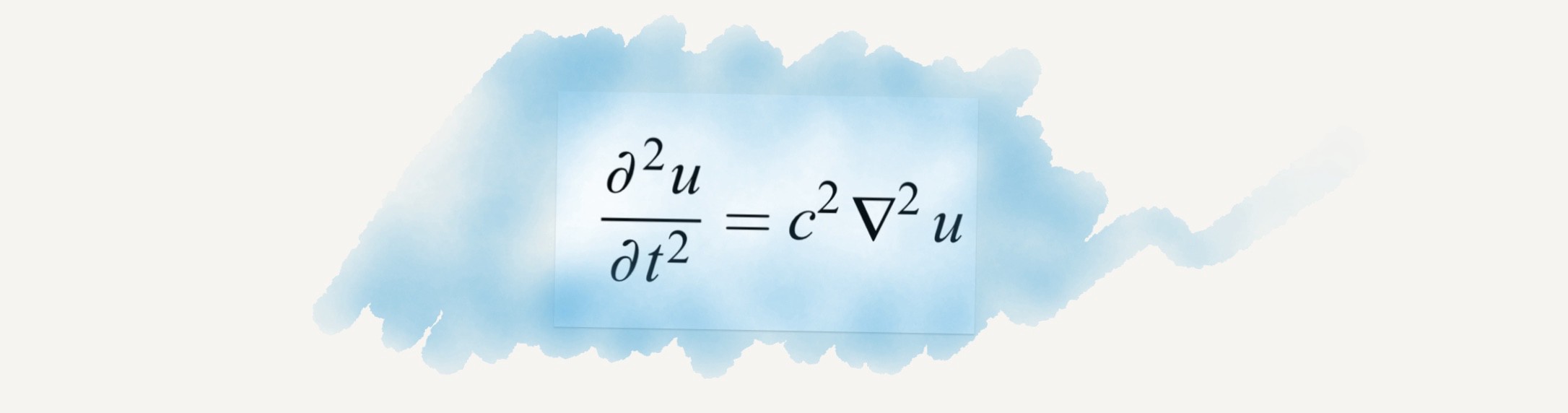
ফুরিয়ার ট্রান্সফর্ম
আপনি যে এই লেখাটি নিজের কম্পিউটার বা স্মার্টফোনের পর্দায় পড়তে পারছেন, এর কৃতিত্ব দিতে হবে ফুরিয়ার ট্রান্সফর্মকে। সকল প্রকার আধুনিক যোগাযোগ ব্যবস্থার মূলে রয়েছে এই ফুরিয়ার ট্রান্সফর্ম। ফুরিয়ার ট্রান্সফর্মের কাজ হলো সিগনাল প্রসেসিং বা বিভিন্ন সংকেত বিশ্লেষণ করা। আমরা এখন ইন্টারনেট ও মোবাইল ফোনের মাধ্যমে দূর-দূরান্তে যোগাযোগ করতে পারি। এখানে আসলে নানা ধরনের তড়িৎচুম্বকীয় ও অন্যান্য সংকেতের আদান-প্রদান ঘটে। ফুরিয়ার ট্রান্সফর্মের বদৌলতে আমরা অনেক তথ্য একত্রে সংকুচিত করে একটি নির্দিষ্ট মাধ্যম দিয়ে চালনা করতে পারি। যোগাযোগ ব্যবস্থার একেবারে মৌলিক বিষয় হলো এই ফুরিয়ার ট্রান্সফর্ম।
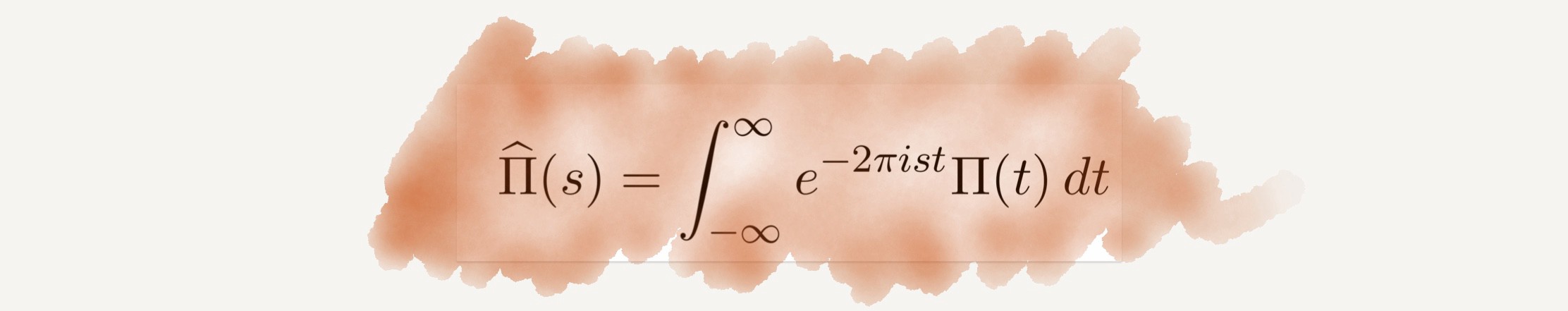

নাভিয়ের-স্টোকস সমীকরণ
তরল পদার্থের প্রবাহ পর্যবেক্ষণের জন্য এই সমীকরণ ব্যবহার করা হয়। যন্ত্রকৌশলের অনেক বড় একটি ক্ষেত্র হলো ফ্লুইড মেকানিক্স। পাইপের মধ্য দিয়ে পানি প্রবাহ, উড়োজাহাজের দুই ডানার মধ্য দিয়ে বাতাসের প্রবাহ, বিদ্যুৎ প্রকল্প থেকে শুরু করে আরো নানা জায়গায় সরাসরি এই সমীকরণের প্রয়োগ ঘটানো হয়। কম্পিউটারে নাভিয়ের-স্টোকস সমীকরণটি বিশেষভাবে প্রোগ্রাম করতে হয়। এরপর উক্ত প্রোগ্রাম ব্যবহার করে প্রকৌশলীরা তরলের উপর পরীক্ষা করেন।
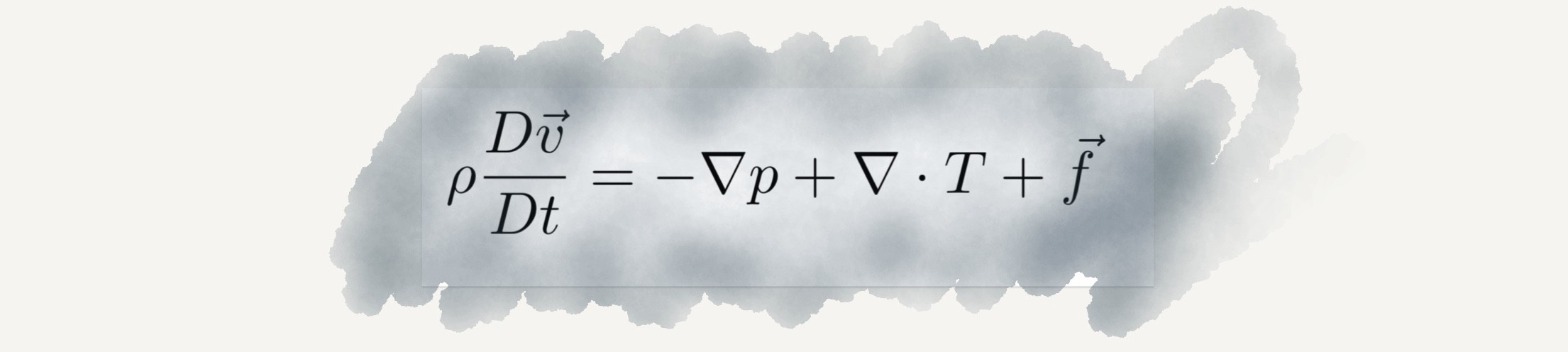
ম্যাক্সওয়েলের সমীকরণ
লৌহদণ্ড তার দিয়ে প্যাঁচানোর পর সেই তারের মধ্য দিয়ে তড়িৎ চালনা করলে লৌহদণ্ডটি চুম্বকে পরিণত হয়। বিজ্ঞানমনস্ক মানুষদের জন্য এটি কোনো নতুন সংবাদ নয়। তবে কেন এটি হয়, তার ব্যাখ্যা দিয়েছেন বিজ্ঞানী ম্যাক্সওয়েল। তার প্রকাশ করা চারটি সমীকরণের সমন্বয়ে এক সেট সমীকরণ রয়েছে। এগুলোকে ম্যাক্সওয়েলের সমীকরণ বলে। কীভাবে তড়িৎ ও চুম্বক শক্তি সম্মিলিতভাবে তাড়িতচুম্বক ক্রিয়া তৈরি করে, তা নিয়েই আলোচনা করা হয়েছে এই সমীকরণগুলোতে। এই তাড়িতচৌম্বক তরঙ্গ যোগাযোগ ব্যবস্থা, চিকিৎসাব্যবস্থা সবকিছুর আমূল পরিবর্তন করে দিয়েছে। আধুনিক পদার্থবিজ্ঞানকে উন্নতির পথে কয়েক ধাপ সামনে নিয়ে গেছে ম্যাক্সওয়েলের সমীকরণ।
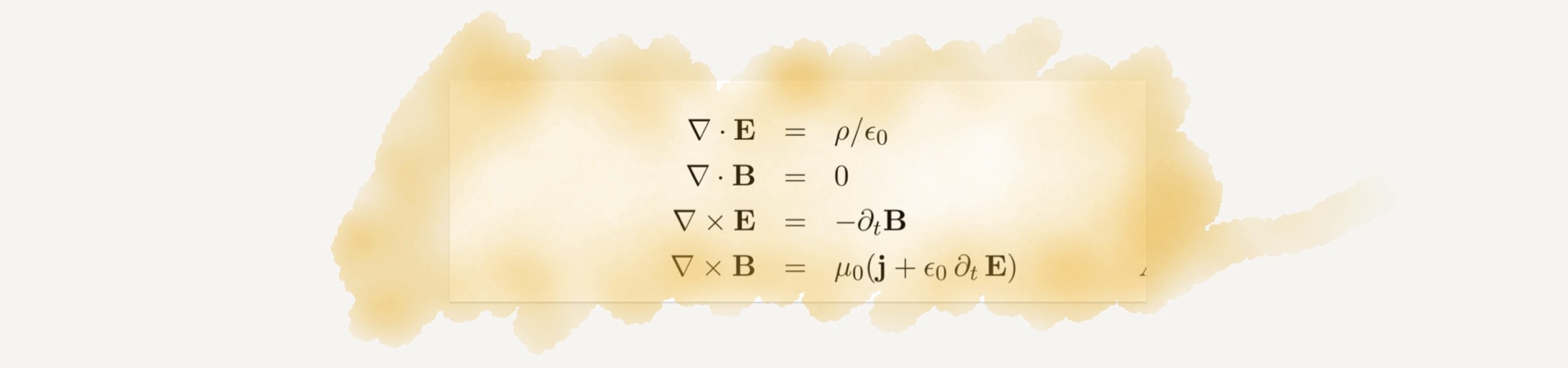
আইনস্টাইনের আপেক্ষিক তত্ত্ব
পদার্থবিজ্ঞানে এক নতুন যুগের সূচনা করেন বিজ্ঞানী আইনস্টাইন। তার বিখ্যাত সূত্র E=mc^2 দিয়ে তিনি পুরো পৃথিবীতে তাক লাগিয়ে দিয়েছিলেন। অতীতের সকল তত্ত্ব বিশেষ করে নিউটনিয়ান পদার্থবিজ্ঞানকে প্রায় অচল করে দিয়েছে আইনস্টাইনের আপেক্ষিক তত্ত্ব। যদিও আমাদের দৈনন্দিন জীবনের সমস্যাগুলোতে সফলভাবে নিউটনিয়ান পদার্থবিদ্যার প্রয়োগ ঘটানো যায়। তবে প্রশ্ন যখন পুরো বিশ্বব্রহ্মাণ্ড নিয়ে আসে, তখন আইনস্টাইনের আপেক্ষিক তত্ত্বের অগ্রাধিকার সবথেকে বেশি। বস্তুত আমরা সময়কে ধ্রুব হিসেবে বিবেচনা করি।
কিন্তু ধরুন, আমরা যদি পৃথিবী থেকে অনেক দূরে, অনেক দ্রুত গতিশীল কোনো স্থানে অবস্থান করি, তাহলে পৃথিবীতে অতিবাহিত সময় ও আমরা যেখানে আছি, সেখানকার সময়ের হিসাবে তারতম্য হবে। আইনস্টাইনের আপেক্ষিক তত্ত্ব স্থান, কাল ও সময়ের হিসাব নিকাশ পুরোপুরি পাল্টে দিয়েছে। মহাবিশ্ব সৃষ্টির বিগ ব্যাং থিওরি, কৃষ্ণগহ্বর, পারমাণবিক শক্তি সবকিছুই যেন এই এক সূত্রে গাঁথা।
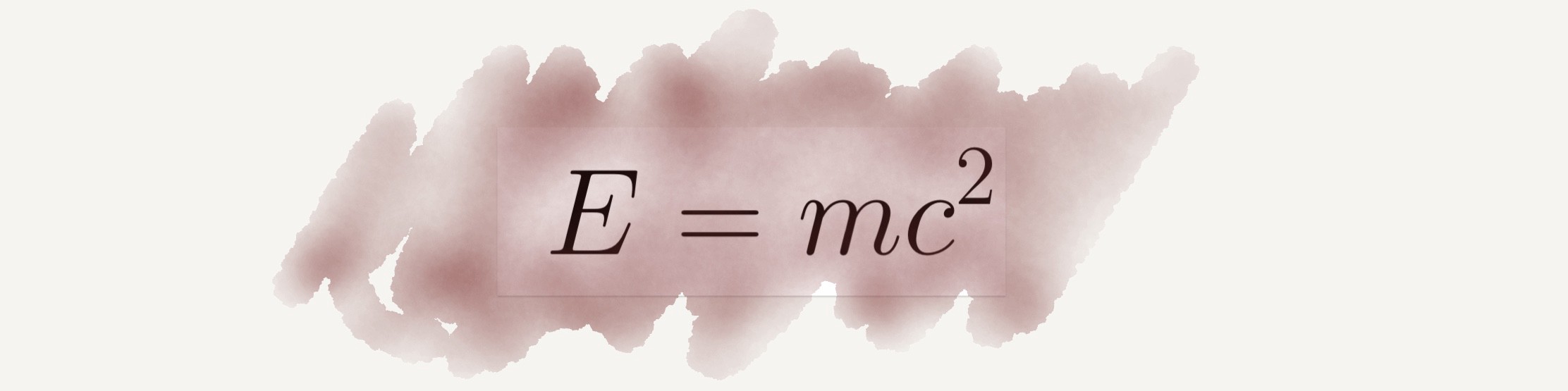
শ্রোডিঞ্জারের সমীকরণ
যেখানে আপেক্ষিক তত্ত্ব অনেক বৃহৎ পরিসরে পুরো মহাজগতের সৃষ্টি ও বিকাশ নিয়ে আলোচনা করে, সেখানে শ্রোডিঞ্জারের সমীকরণ আলোচনা করে একেবারে ক্ষুদ্র অণু-পরমাণুর আচরণ সম্পর্কে। কোয়ান্টাম তত্ত্বের মূল ভিত্তিই হলো শ্রোডিঞ্জারের সমীকরণ। আধুনিক পদার্থবিজ্ঞানের চেহারাই বদলে দিয়েছে আপেক্ষিক তত্ত্ব ও শ্রোডিঞ্জারের সমীকরণ। আমাদের আধুনিক প্রযুক্তির জন্য এক শক্ত ভিত তৈরি করে দিয়েছে কোয়ান্টাম তত্ত্ব। পারমাণবিক শক্তি, কোয়ান্টাম কম্পিউটার, লেজার রশ্মি সহ আরো বিভিন্ন ক্ষেত্রে উন্নতি সাধন করেছে এই তত্ত্বটি।
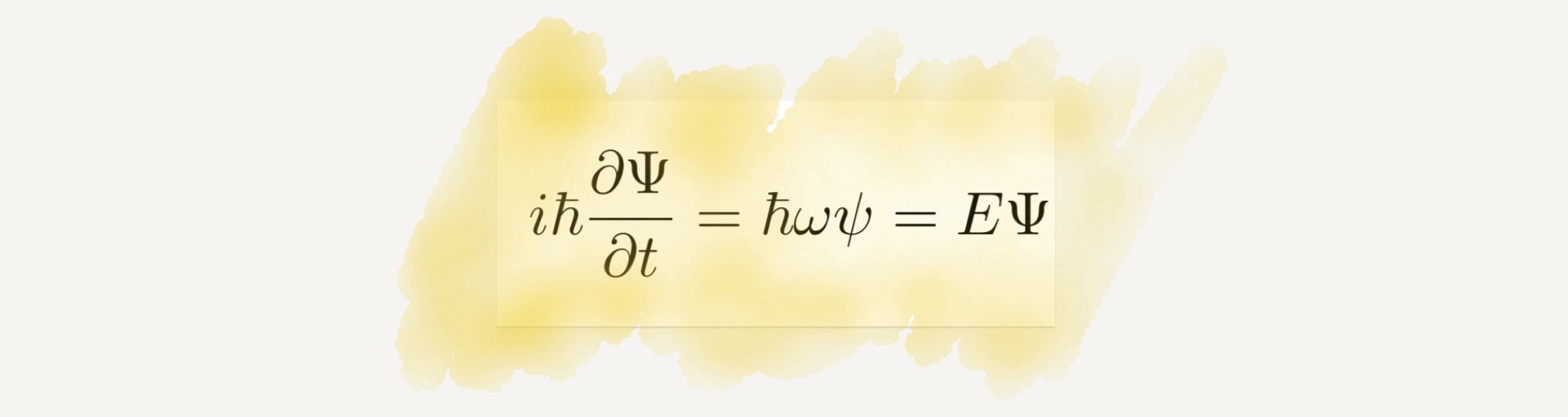
ইনফরমেশন থিওরি
ফুরিয়ার ট্রান্সফর্মের কথা আমরা আগেই বলেছি। যোগাযোগ ব্যবস্থায় যেসব সিগনাল বা সংকেত আদান-প্রদান হয়, তা ফুরিয়ার ট্রান্সফর্ম ব্যবহার করে বিশ্লেষণ করা যায়। তবে আধুনিক যোগাযোগ ব্যবস্থার ক্ষেত্রে একটি বিরাট সমস্যা ছিল, কীভাবে এত বিপুল পরিমাণ তথ্য এক জায়গা থেকে আরেক জায়গায় পাঠানো সম্ভব, তা নিয়ে। এখানেই কৃতিত্ব দিতে হবে ইনফরমেশন থিওরিকে। ইনফরমেশন থিওরি প্রয়োগ করে আমরা যেকোনো তথ্য যথাসম্ভব সংকোচন করে আদান-প্রদান করতে পারি। এতে করে তথ্যের কোনো ক্ষতি না করেই তা সঠিকভাবে ও দ্রুত পাঠানো সম্ভব। আধুনিক কম্পিউটার নেটওয়ার্কের মূল ভিত্তি হলো এই ইনফরমেশন থিওরি।
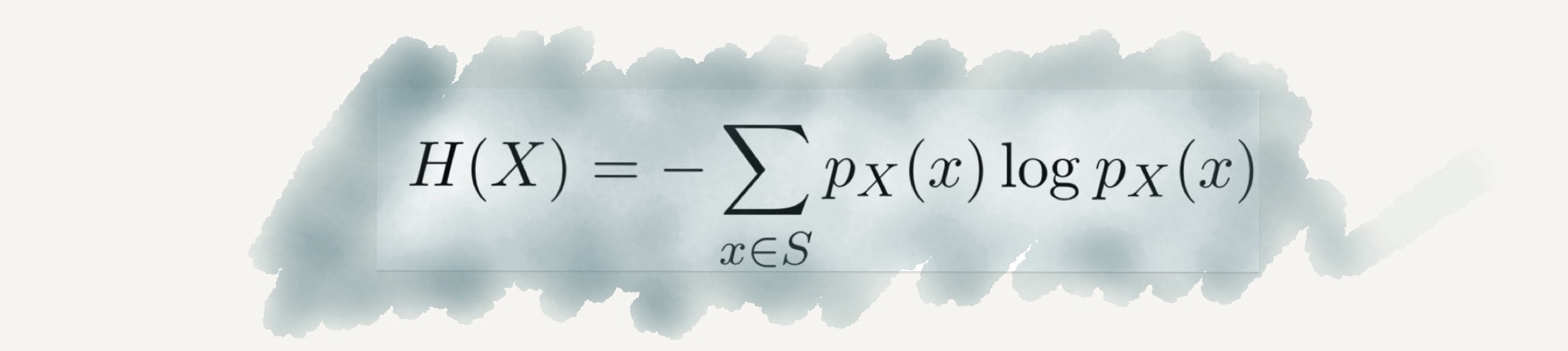
ক্যাওস থিওরি
এই সমীকরণ একটি মানচিত্রের উপর নির্ভর করে। এই মানচিত্রে কোনো নির্দিষ্ট মান সময়ের সাথে কীভাবে পরিবর্তিত হয়, তা পর্যালোচনা করা হয়। একটি নির্দিষ্ট জায়গায় কোনো বস্তুর একটি নির্দিষ্ট মানের জন্য যে বিশৃঙ্খল পরিস্থিতি তৈরি হয়, তা এই তত্ত্ব দিয়ে ব্যাখা করা যায়। এই ক্যাওস থিওরি মূলত প্রয়োগ করা হয় ভৌগোলিক আবহাওয়া পর্যবেক্ষণ ও আবহাওয়ার পূর্বাভাস প্রদানের কাজে।
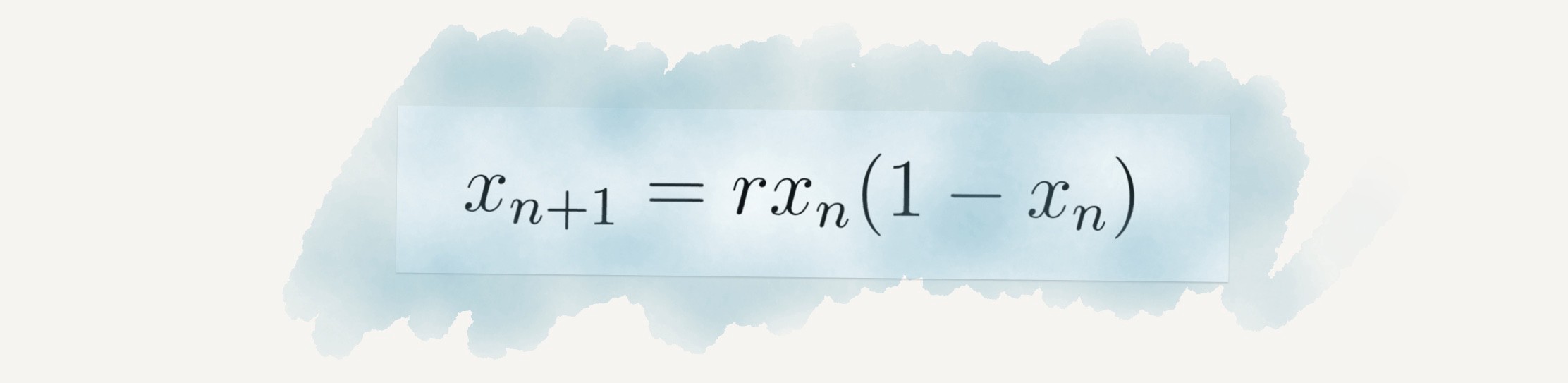
ব্ল্যাক–শোলস সমীকরণ
আমাদের নিত্যপ্রয়োজনীয় দ্রব্যাদির প্রায়ই দ্রব্যমূল্য হ্রাসবৃদ্ধি ঘটতে থাকে। এই দ্রব্যমূল্যের ওঠানামা নির্ভর করে বিভিন্ন ঘটনাকে কেন্দ্র করে। অর্থনীতিবিদরা ব্ল্যাক–শোলস সমীকরণটি ব্যবহার করেন মূলত কোনো বস্তুর বাজারদরের এই পরিবর্তন পর্যালোচনা করার জন্য। শেয়ার বাজারের পরিস্থিতি, বিভিন্ন বৈশ্বিক ঘটনার পরিপ্রেক্ষিতে কীভাবে এই পরিবর্তনগুলো ঘটে, তা হিসাব করা যায় এই সমীকরণের মাধ্যমে। এতে করে কখন কোন দ্রব্যের চাহিদা বাড়বে আর কোনটির চাহিদা হ্রাস পাবে, তা সহজে যাচাই করা সম্ভব।
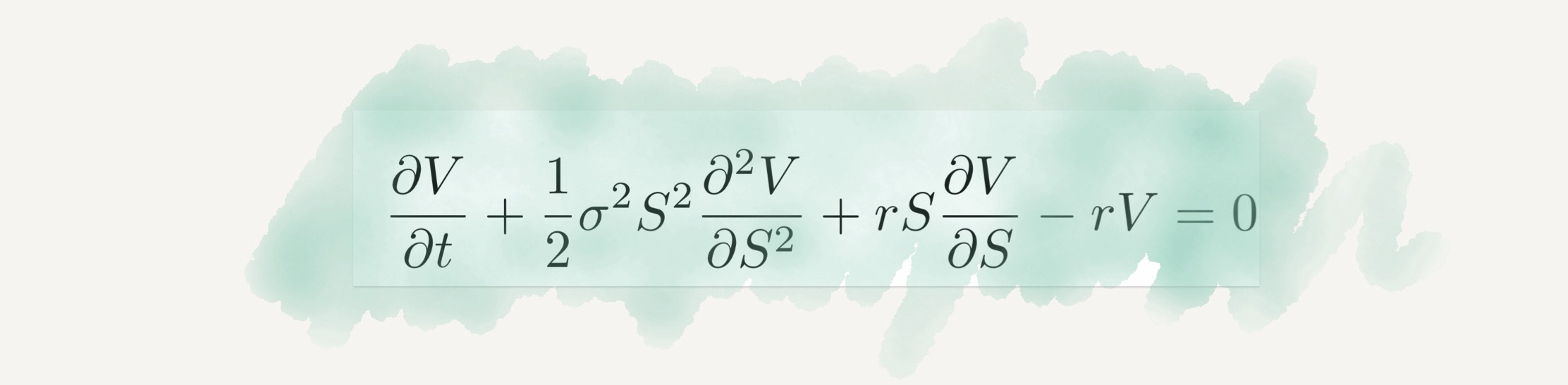
শেষ কথা
সমীকরণগুলোর অভ্যন্তরীণ জটিলতার কারণে তা নিয়ে এখানে বিস্তারিত আলোচনা করা সম্ভব নয়। তবে এটা বলার অপেক্ষা রাখে না যে, আমাদের পৃথিবীতে এগুলোর তাৎপর্য কত বেশি। বিজ্ঞানীরা সবসময় চেষ্টা করেন প্রকৃতির রহস্য উন্মোচনের। তাদেরকে এসব রহস্য থেকে একটি বাস্তবসম্মত ব্যাখ্যা তৈরি করতে হয়। আর সেই ব্যাখ্যা কাগজে-কলমে দাঁড়া করানোর জন্যই এসব সমীকরণের আবির্ভাব ঘটে।