পুরকৌশলের প্রাথমিক ধারণা || পর্ব ৩ || দালান তৈরিতে কেন মাধ্যাকর্ষণের হিসাব গুরুত্বপূর্ণ

ভার বা লোড কী?

বিজ্ঞান বা প্রকৌশলের এমন কিছু জিনিস আছে যা আমজনতার কাছে পানির মতো পরিষ্কার হয়ে ধরা পড়ে। ভার বা ওজন হলো সেসব ধারণাগুলোর একটি। এক টুকরো পাথর এবং একটিমাত্র বাদামের মধ্যে কোনটাকে হাতে নিলে বেশি ভারী মনে হবে তা যেকোনো মানুষই জানেন। এমনকি এটা বোঝার জন্য বস্তু দুটি হাতে নেয়ারও হয়তো প্রয়োজন পড়বে না। জন্মের পর থেকে এ পর্যন্ত বড়, ছোট, কদাকার, সুষম, বিভিন্ন ধরনের বস্তু দেখে দেখে মানুষের মস্তিষ্কে একটি ধারণা হয়ে গেছে যে, কোন ধরনের বস্তুর ভার কেমন হতে পারে।

দূর থেকে দেখেই বলে দেয়া যায় একটি রিক্সা ভ্যান ও একটি ট্রাকের মধ্যে কোনটা ভারী হবে। এক্ষেত্রে ট্রাকের আকার বড়, ভ্যানের আকার ছোট। বস্তু দুইটির আকৃতিগত পার্থক্য থেকে এই যে ভার আন্দাজ করার ক্ষমতা আমরা পেয়েছি, একে বলে ‘অভিজ্ঞতালব্ধ জ্ঞান’ (Empirical Knowledge)। এ জ্ঞানের কারণেই নদীর পাড় কোথায় কখন ভাংতে পারে তা একজন প্রকৌশলীর চেয়ে সেই এলাকায় গত বিশ-ত্রিশ বছর ধরে বসবাস করা গ্রামবাসী অনেক ভালোভাবে বলতে পারেন।

কোন মাটিতে কোন ফসল রোপণ করলে অধিক ফলন পাওয়া যাবে, তা তারাই ভালো বলতে পারবে, যারা তাদের পূর্বপুরুষদের সময় থেকে সে জমি চাষ করে আসছেন। সে মাটির প্রতিটি কণা, গন্ধ ও রঙের সাথে তারা সুপরিচিত। আবার কখন স্বাভাবিক সময়ের ব্যতিক্রম কিছু হতে পারে তাও তাদের অভিজ্ঞতালব্ধ জ্ঞান থেকে বেশ ভালোভাবে জানে। যেমনঃ একটি বেলুনকে যতই বাতাস দিয়ে ফোলানো হোক না কেন তার ভার সমআকৃতির কোনো লোহার গোলকের সমান হতে পারে না। জীবনে একবার হলেও বেলুন দেখেছেন বা ধরেছেন এমন মানুষ মাত্রই এটা জানে। তিনি জানেন, সবসময় বস্তুর আকৃতির উপরই তার ভার নির্ভর করে না। বস্তুর ভেতরে পদার্থের পরিমাণ কতটুকু তাও এখানে একটি বিবেচ্য বিষয়।

আবার ভারের অনুভূতি একেক মানুষের কাছে একেক রকম হতে পারে। একজন শক্তিশালী মানুষের কাছে যে ভার হালকা মনে হবে, সেই ভারই একজন কৃশকায় মানুষের কাছে ভারী মনে হবে। অনুভূতি ব্যাপারটিই ব্যক্তিভেদে আপেক্ষিক, একে মাপা যায় না। কিন্তু বিজ্ঞান চায় সুস্পষ্ট পরিমাপ, যা স্থান, কাল, পাত্র নির্বিশেষে সকলের কাছে একই থাকবে। এ কাজটি কীভাবে করা হয়? কীভাবে আমরা বস্তুর ভার গাণিতিকভাবে মেপে নিরপেক্ষভাবে বলতে পারবো কোনটা ভারী আর কোনটা হালকা?

মহাকর্ষের ধারণা

বিজ্ঞানী আইজ্যাক নিউটন তার উপলব্ধি এবং গাণিতিক হিসাব নিকাশ থেকে সিদ্ধান্তে আসলেন, বিশ্বের প্রতিটি বস্তুই একে অপরকে তার নিজের দিকে আকর্ষণ করে। উভয় আকর্ষণ যুগপৎ ঘটছে, এমন নয় যে একের আকর্ষণ শেষ হবার পরে অন্যজন আকর্ষণ করা শুরু করেছে, পুরো ঘটনা একই সময়ে ঘটছে। আবার এ আকর্ষণ ঘটে একেবারে সরলরেখা বরাবর, কোনো আঁকাবাকা পথে নয়। এই আকর্ষণ বলকে বলা হয় ‘মহাকর্ষ বল’ (Gravitational Force)।

মনে কিছু প্রশ্ন আসতে পারে। যদি জগতের প্রতিটি বস্তু একে অপরকে মহাকর্ষীয় বলের মাধ্যমে আকর্ষণ করেই থাকে তাহলে আমরা তা অনুভব করতে পারি না কেন? আবার যদি আকর্ষণ হয়েই থাকে তাহলে একে অন্যের দিকে বস্তুগুলো ছুটে যায় না কেন? প্রথম প্রশ্নের উত্তর হলো, একটি চুম্বক যখন অন্য একটি চুম্বক বা চৌম্বক পদার্থকে আকর্ষণ করে তখন সেটা খালি চোখে দেখা যায়, আমরা আমাদের দৃষ্টিশক্তির মাধ্যমে অনুভব করতে পারি যে এরা একে অপরকে নিজেদের দিকে আকর্ষণ করছে। এভাবে আমাদের কাছে চৌম্বক শক্তির অস্তিত্ব বিশ্বাস করে নিতে খুব একটা কষ্ট হয় না। এদের মধ্যকার আকর্ষণ বল বেশ তীব্র হয়, আর এ কারণেই তা আমরা খালি চোখে অনুভব করতে পারি।

চৌম্বক বলের তুলনায় মহাকর্ষ বলের টান অনেক কম। মহাজগতের সকল বলকে যে চারটি ভাগে ভাগ করা হয়েছে তার মধ্যে মহাকর্ষ হলো সবচেয়ে দূর্বল। কাজেই এর অস্তিত্ব খালি চোখে টের না পাওয়াই স্বাভাবিক। তবে হ্যাঁ, বস্তু যত বড় হয়, তাদের মধ্যকার মাধ্যাকর্ষণ শক্তির মানও ততই বাড়তে থাকে। অর্থাৎ একজন মানুষ অন্য একজন মানুষকে যে বলে আকর্ষণ করছে তা বোঝা বেশ কঠিন হলেও, সূর্য পৃথিবীকে বা পৃথিবী একজন মানুষকে যে বলে আকর্ষণ করছে তা দূর থেকে দেখে শুধুমাত্র দৃষ্টিশক্তির সাহায্যে খুব সহজেই অনুধাবন করা যায়। এ বলের কারণেই একজন মানুষ পৃথিবীর পৃষ্ঠ বা মাটি থেকে লাফ দিলে পৃথিবী থেকে ছিটকে বের হয়ে যান না, পৃথিবী তাকে টেনে নিজের দিকে ধরে রাখে।

 

পৃথিবী ও অন্য যেকোনো বস্তুর মধ্যে যে আকর্ষণ বা মাধ্যাকর্ষণ বল কাজ করে তার একটি বিশেষ নাম আছে, একে বলে ‘অভিকর্ষ বল’ (Gravity)। এখানে স্বাভাবিকভাবেই যে খটকা লাগে তা হলো, মাধ্যাকর্ষণ বা অভিকর্ষ যাই বলা হোক, তার মানেই হলো বস্তুদ্বয় একে অপরকে ‘সমান’ বলে নিজের দিকে আকর্ষণ করছে। অর্থাৎ পৃথিবী একজন মানুষকে যে বলে আকর্ষণ করছে, মানুষও পৃথিবীকে ঠিক সেই পরিমাণ বলেই নিজের দিকে আকর্ষণ করছে।

তাহলে আকর্ষণ বল যদি উভয়ের সমান হয়েই থাকে, মানুষ কেন পৃথিবীর দিকে ছুটে যায়? পৃথিবী কেন মানুষের দিকে ছুটে আসে না। এ ব্যাপারটা বেশ কৌতূহলোদ্দীপক। মানুষ যখন মাটি থেকে লাফ দেয়, সে আবার অভিকর্ষের টানে পুনরায় মাটিতেই ফিরে আসে। মাটি মানুষের কাছে ফিরে যায় না। এর ব্যাখ্যাটা হলো, মাধ্যাকর্ষণ বা এক্ষেত্রে অভিকর্ষে সেই বস্তুই আধিপত্য বিস্তার করবে যার ভর বেশি। ভারী বস্তুর দিকে হালকা বস্তু সর্বদা ছুটে যাবে যদিও তাদের মধ্যকার আকর্ষণ বল সমান। পৃথিবী ও মানুষের মধ্যে পৃথিবী তুলনামূলকভাবে মানুষের তুলনায় অধিক ভারী। তাই মানুষ পৃথিবীর দিকে ছুটে আসে এবং উল্টো ঘটনা ঘটে না।

একটি দালানকে তার জন্মের পর থেকে ধ্বংসের আগ অবধি যে একটি মাত্র শক্তির বিরুদ্ধে প্রতিনিয়ত যুদ্ধ করতে হয় তা হলো ‘অভিকর্ষ বল’ বা ‘ওজন’। দালানে মানুষ বসবাস করে, তাদের ওজন আছে। সেই মানুষেরা বিভিন্ন আসবাবপত্র ব্যবহার করে তার ওজন আছে। কিছু কিছু দালানে একই সময়ে অনেকজন মানুষ একসাথে জড়ো হয়, যেমনঃ শপিং কমপ্লেক্স, বিদ্যালয়, প্রভৃতি। কিছু দালানে শিল্পভিত্তিক কাজের জন্য বেশ ভারী ভারী যন্ত্রপাতি বসানো হয়, যেমনঃ তৈরি পোশাক কারখানা, রাসায়নিক সামগ্রী নির্মাণের কারখানা, প্রভৃতি। এভাবে একেক ধরনের দালানকে তার জীবনকালে ভেতরে থাকা একেক ধরনের ভারকে সামাল দিতে হয়। এজন্য ওইসব দালানের অবকাঠামোগত নকশাও একেক ধরনের হয়ে থাকে।

তবে দালানের ভেতরে থাকা এতসব ওজন বহন করা তার জন্য বেশ ঠুনকো ব্যাপার। এর চেয়েও ভয়াবহ আরেক ধরনের ওজনের বিরুদ্ধে তাকে সার্বক্ষণিক লড়তে হয়। চোখের সামনে থাকা ওজন দেখতে দেখতে এবং তা নিয়ে বিশ্লেষণ করতে করতে আমরা হয়তো ভুলে যাই চোখের আড়ালে থাকা সেই ভয়ংকর শত্রুর কথা। দালানের উপর সবচেয়ে বেশি পরিমাণে যে ওজন আসে তা কোনো ভারী সেগুন কাঠের আলমারী থেকে নয়, নয় কোনো ডায়াল গেজওয়ালা কদাকার টনকে টন ভারী কম্প্রেশন টেস্টিং মেশিন থেকে, সেই ওজন হলো দালানের নিজের ওজন বা Self Weight।

নিজস্ব ওজন (Self Weight)

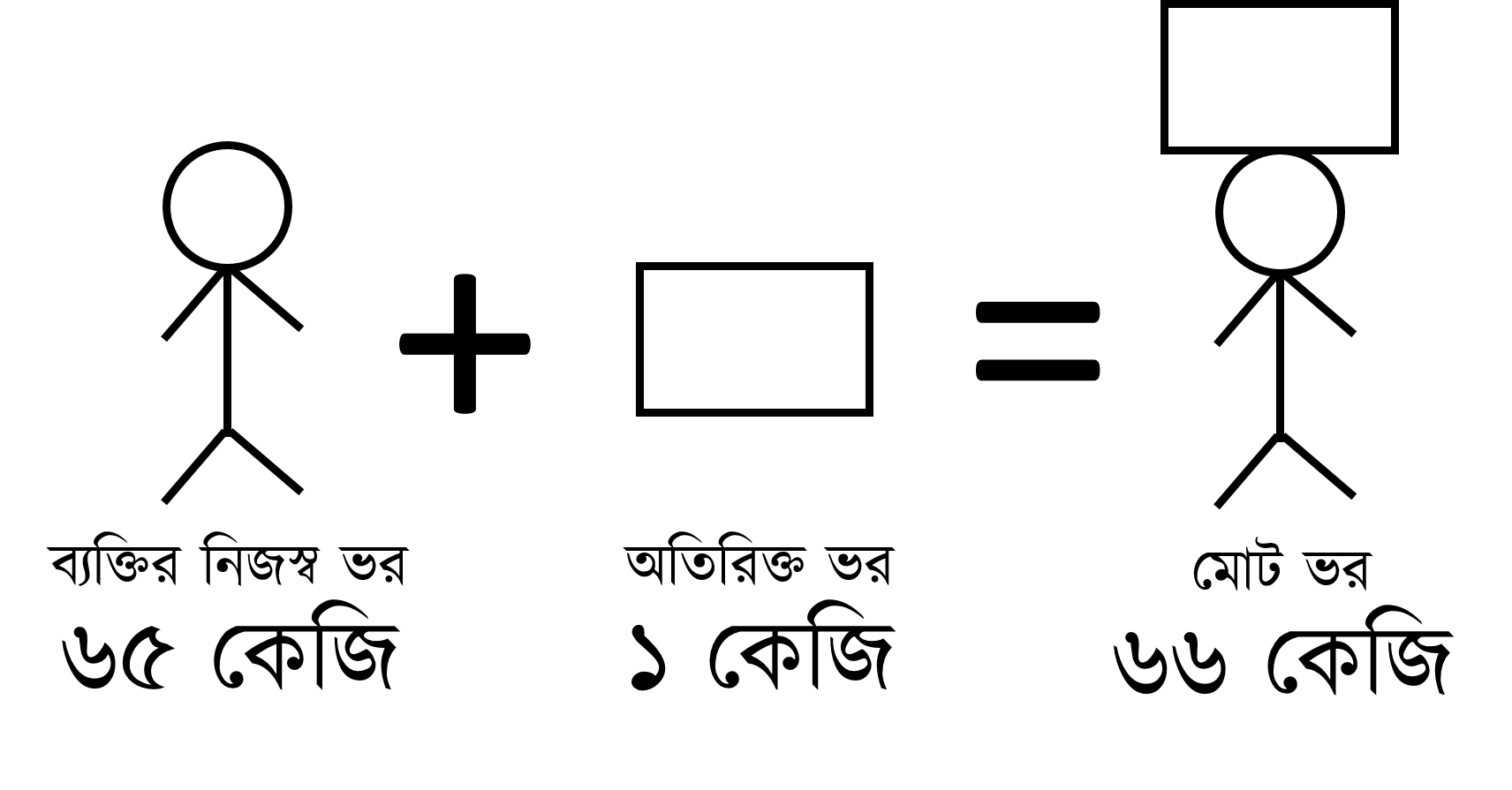
একজন মানুষের হাতে যদি ১ কেজি ভরের একটি বস্তু দিয়ে তাকে মাটির উপর দাঁড় করিয়ে দেয়া হয়, তাহলে সাধারণভাবে আমরা ধরে নিই মাটির উপর ওই ১ কেজি ভরের বস্তুটির ওজনই শুধুমাত্র চালান হচ্ছে। এক্ষেত্রে যে ওজন হিসেবের কথা আমরা ভুলে যাই তা হলো ঐ ব্যক্তির নিজের ওজন। ধরি যার হাতে একটু আগে ১ কেজি ভরের বস্তুটি দেয়া হয়েছিল, ঐ ব্যক্তির ভর ৬৫ কেজি। এখন যদি জিজ্ঞেস করা হয় উনি যে জায়গায় দাঁড়িয়ে আছেন সে জায়গার উপর কতটুকু ভর তার ওজন চালান করে দিচ্ছে? উত্তর হবে ৬৫ কেজি + ১ কেজি = ৬৬ কেজি ভরের ওজন সেখানকার মাটির উপর দেয়া হচ্ছে।

বলা যেতে পারে, ব্যক্তির এই ৬৫ কেজি ভর থেকে প্রযুক্ত ওজন হচ্ছে তার ‘নিজস্ব ওজন’। খেয়াল করলে দেখা যাবে, শুরুতে দেয়া ১ কেজি ভরের তুলনায় ব্যাক্তির এই নিজস্ব ভর থেকে প্রযুক্ত ওজন কিন্তু অনেক বেশি, ৬৫ গুণ। কাজেই একে অগ্রাহ্য করার কোনো সুযোগ নেই। দালানের বেলাতেও একই কথা খাটে। দালান তার উপর বোঝাই করা মানুষ, তাদের আসবাবপত্র, ছাদের পানির ট্যাংক, সিড়িঘরের জিনিসপত্র, প্রভৃতি মাথায় করে দাঁড়িয়ে আছে। একজন প্রকৌশলীকে দালানের নকশা করার সময় আগেই হিসেব করতে হয় এই দালানটিতে কোন কোন জিনিস থেকে ভার আসতে পারে। সাথে দালানটির নিজস্ব ওজন কত হবে তাও হিসেব করে পুঙ্খানুপুঙ্খভাবে গাণিতিক হিসেব কষতে হয়।

দালানের কোথায় কোথায় হতে তার নিজস্ব ওজন আসতে পারে তা বিবেচনা করা যাক। মানুষের যেমন হাত, পা, পেট, মাথাসহ আরো নানা প্রকার অঙ্গ-প্রত্যঙ্গ রয়েছে, দালানেরও এরকম বিভিন্ন অংশ থাকে, যেখান থেকে পৃথক পৃথকভাবে ওজন দালানের নিচে অবস্থিত মাটিতে চালান হয়, যেমনঃ কলাম, বিম, স্ল্যাব, এসবের ভেতরে অবস্থিত রড, প্রভৃতি।

তবে একজন মানুষ মাটির উপর দাঁড়িয়ে যেভাবে তাতে ওজন চালান করে দেয়, দালান হুবহু সেভাবে তা করে না। ওজন চালানের দিক থেকে এ দু’য়ের মাঝে গুণগত কিছু পার্থক্য রয়েছে। ঐ ব্যক্তি যখন মাটির উপরে দাঁড়িয়ে আছেন তখন তিনি ভর প্রদান করছেন খুব ছোট একটি জায়গার উপর, বলা যেতে পারে তার দুই পায়ের নিচের যতটুকু জায়গায় মাটি আছে ঠিক ততটুকু জায়গায়। ধরা যাক তিনি একটি মাঠে দাঁড়িয়ে আছেন। তাহলে পুরো মাঠের মোট জায়গার তুলনায় তার পায়ের নিচের জায়গাটা কিন্তু অনেক ছোট, একেবারে বিন্দুর মতো।

এভাবে গোটা ভর যখন শুধুমাত্র একটি বিন্দুর উপর প্রয়োগ করা হয়, বা সোজা কথায় পুরো বস্তুটি যখন শুধুমাত্র একটি বিন্দুর উপর দাঁড়িয়ে থাকে তখন যে ওজন অনুভূত হয়, তাকে বলে ‘বিন্দু ভার’ (Point Load)। যেমনঃ ধরা যাক, আমাদের ফুলদানি একটি সুনির্দিষ্ট জায়গায় তুলনামূলকভাবে একটি বিন্দুর উপর তার ভার প্রদান করছে, কাজেই সেটি একটি বিন্দু ভার। বাসার ভেতরে মানুষেরা আছেন, তারা কখনো কখনো এক জায়গায় স্থির হয়ে দাঁড়িয়ে আছেন, তারা একেকটি বিন্দু ভার হিসেবে বিবেচিত হতে পারেন। একটি সুনির্দিষ্ট জায়গায় অবস্থিত বিন্দু ভার প্রদানকারী কোন বস্তু আসলে কতটুকু ভার প্রদান করছে তা গাণিতিকভাবে বের করা যায় নিউটনের গতি সংক্রান্ত দ্বিতীয় সূত্র ধরে। যদি কোনো বস্তুর ভর হয় ৬৫ কেজি, তাহলে একে ঐ স্থানের অভিকর্ষজ ত্বরণ, যা আদর্শ হিসেব অনুসারে ৯.৮ মি./সেকেন্ড^(^২), দ্বারা গুণ করে বস্তুর ওজন হিসেব করা হয়। উল্লেখ্য যে, বস্তুর ওজন পরিমাপের আন্তর্জাতিক একক হলো ‘নিউটন’। এক্ষেত্রে ওজন হবে,

৬৫ কেজি X ৯.৮ মি./সেকেন্ড^(^২) = ৬৩৭ নিউটন

আমরা সাধারণত বাড়িতে ওজনমাপক যন্ত্রে আমাদের যে ওজন মাপি তা হলো ‘বিন্দু ভার’ বা ‘বিন্দু ওজন’। এবার কল্পনা করা যাক, একটু আগে যে ব্যক্তি মাঠে একটি ছোট জায়গার উপর দাঁড়িয়ে ছিলেন, এখন তিনি আর দাঁড়িয়ে নেই, শুয়ে পড়েছেন ক্লান্ত হয়ে। পুরো দৃশ্যটি এখন খুব ভালো করে পর্যবেক্ষণ করা প্রয়োজন। এখন কিন্তু সেই ব্যক্তি আর ছোট এক জায়গার উপর তার ভর দিচ্ছেন না যাকে বিন্দু হিসেবে চাইলেই বিবেচনা করা যাবে। এখন যেহেতু তিনি শুয়ে পড়েছেন, তার মানে বেশ বড় একটি জায়গার উপর তিনি তার ভার প্রদান করছেন। বলা যায়, তিনি এখন আর একটি বিন্দুর উপর নয়, বরং ঐ বিন্দুটির মতো আরো অসংখ্য বিন্দুর উপর একইসাথে ভার প্রদান করছেন। কাজেই একে আগের মতো বিন্দু ভার হিসেবে বিবেচনা করলে চরম ভুল হবে। যদিও তিনি কিন্তু এখনো শুয়ে শুয়ে মাটির উপর ৬৩৭ নিউটন বলই প্রদান করছেন, তবে আগের থেকে একটু ভিন্নভাবে। প্রশ্ন হলো, এই যে ভিন্নভাবে এখন ওজনের হিসেবটা করতে হচ্ছে একে গাণিতিকভাবে কীভাবে প্রকাশ করা যেতে পারে?

সমবণ্টিত ভার (Uniformly Distributed Load)

৬৫ কেজি ভরের যে ব্যক্তির কথা এতক্ষণ ধরে আলোচনা করা হচ্ছে, এবার ধরা যাক তাঁর উচ্চতা ২ মিটার। তিনি এখন ক্লান্ত পরিশ্রান্ত, মাটিতে সটান হয়ে শুয়ে আছেন। ধরে নেয়া যায়, তাঁর শরীরের ২ মিটারের নিচে অবস্থিত সবটুকু মাটিতে তার ৬৫ কেজি ভর থেকে উদ্ভূত ৬৩৭ নিউটন ওজন একেবারে সমানভাবে বণ্টিত হচ্ছে। ৬৩৭ নিউটন ওজন, ২ মিটার দৈর্ঘ্যের মাটি। তাহলে প্রতি একক মাটিতে কতটুকু ওজন চালান করা হচ্ছে?

৬৩৭ নিউটন ÷ ২ মিটার = ৩১৮.৫ নিউটন/মিটার

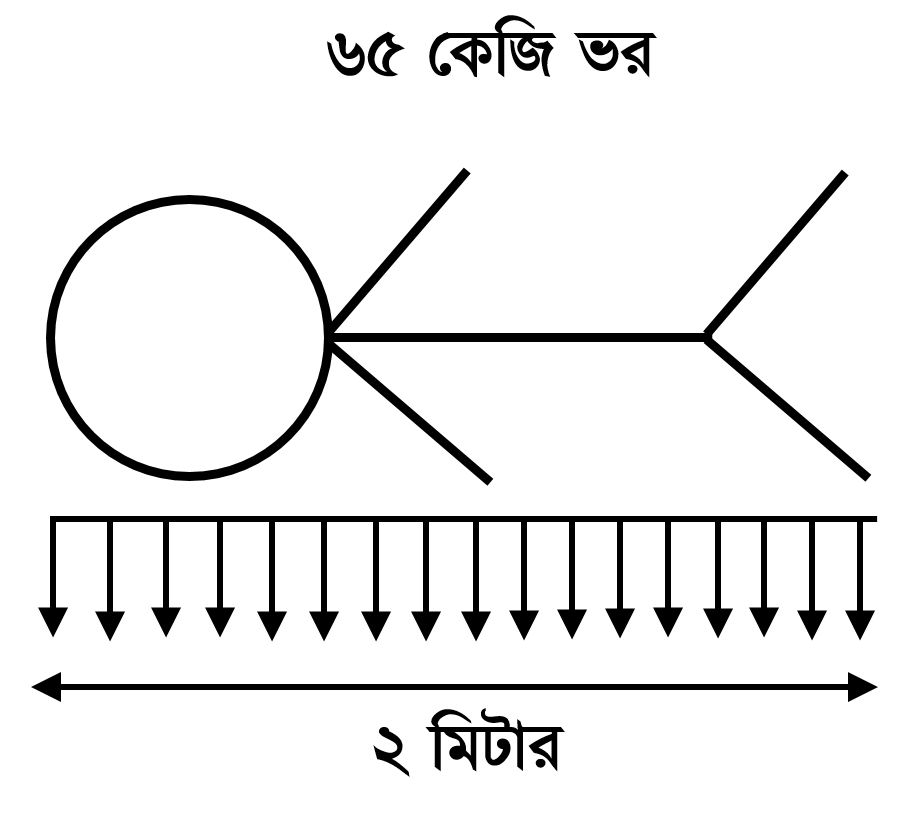
এই ওজন বিন্দু ভার থেকে সম্পূর্ণ আলাদা। বিন্দু ভার একটি বিন্দুর উপর প্রযুক্ত হয়, প্রকাশ করা হয় নিউটন এককে। এই নতুন ধাঁচের ওজন প্রযুক্ত হচ্ছে একটি নির্দিষ্ট দৈর্ঘ্যের উপর, এক্ষেত্রে তা ২ মিটার, প্রকাশ করা হচ্ছে নিউটন/মিটার এককে। কাজেই দুটিকে একই জিনিস মনে করার কোনো কারণ নেই। এ নতুন ধাঁচের ওজনের নাম হলো, ‘সমবণ্টিত ভার’ বা Uniformly Distributed Load (UDL)। দালানের বিভিন্ন জায়গায় এ ধরনের ভার দেখা যেতে পারে। এর একটি ভালো উদাহরণ হলো দালানের বিমসমূহ। এরা ঠিক সেভাবেই দালানের বিভিন্ন জায়গায় শুয়ে আছে যেভাবে উদাহরণের এই ব্যক্তি শুয়ে ছিলেন। তাদের যে ওজনটা মাটিতে যাচ্ছে সেটাও ‘সমবণ্টিত ভার’ হিসেবেই মাটিতে যাচ্ছে, ‘বিন্দু ভার’ হিসেবে নয়।

একটি জিনিস বলে রাখা প্রয়োজন, সমবণ্টিত ভার এখানে একটি দৈর্ঘ্যের উপর প্রয়োগ করা হয়েছে, যার মান ২ মিটার। সবসময় যে তা শুধুমাত্র দৈর্ঘ্যের উপরেই প্রয়োগ করা হবে এমন নয়, তা একটি ক্ষেত্রের উপর, এমনকি একটি আয়তনের উপরও প্রয়োগ করা যেতে পারে। সহজ করে বললে, যখন বলা হচ্ছে, ঐ ব্যক্তি মাটির উপর ৩১৮.৫ নিউটন/মিটার ওজন প্রয়োগ করছেন তখন ধরে নেয়া হচ্ছে তিনি ঐ মাটির উপর একটি সরলরেখা বরাবর শুয়ে আছেন, একটুও কাঁত হননি। যদি তিনি কাঁত হয়ে মাটির উপর ছড়িয়ে শুয়ে থাকেন তাহলে ওজনটা ৩১৮.৫ নিউটন/মিটার হবে না, একে আবার একটু অন্যভাবে আমাদের চিন্তা করতে হবে। ধরে নিই, তিনি এখন মাটির উপর একটি আয়তক্ষেত্রে শুয়ে আছেন, যার দৈর্ঘ্য ৩ মিটার ও প্রস্থ ২ মিটার। অতএব,

ক্ষেত্রফল = ৩ মিটার X ২ মিটার = ৬ বর্গমিটার

অর্থাৎ এখন ঐ ৬৫ কেজি ভরের (৬৩৭ নিউটন ওজন) ব্যক্তির ওজন প্রয়োগ করা হচ্ছে ৬ মিটার২ জায়গার একটি ক্ষেত্রের উপর, আগের মতো ২ মিটারের একটি সরলরেখার উপর নয়। এখন পূর্বের মতো সমবণ্টিত ভর হিসেব করলে এভাবে হিসেব করতে হবে,

৬৩৭ নিউটন/৬ বর্গমিটার = ১০৬.১৭ নিউটন/মিটার^(^২) (প্রায়)

সাধারণত দালানের বিভিন্ন জায়গার স্ল্যাবের ওজন এভাবে ক্ষেত্র ধরে হিসেব করা হয়ে থাকে। যেমনঃ শয়নকক্ষের মেঝে, খাবার ঘরের মেঝে, রান্নাঘরের মেঝে, প্রভৃতি। বাকি রইলো আয়তনের হিসেব। ধরা যাক, তিনি এখন একটি ঘনবস্তুর উপর শুয়ে আছেন। যাদের ঘনবস্তু সম্পর্কে ধারণা নেই, একটি সরলরেখার একটি মাত্র মাত্রা থাকে, সেটা দৈর্ঘ্য। একটি আয়তক্ষেত্রের থাকে দুইটি, দৈর্ঘ্য ও প্রস্থ। একটি ঘনবস্তুর ক্ষেত্রে দৈর্ঘ্য ও প্রস্থের পাশাপাশি আরো একটি মাত্রা থাকে, তা হলো উচ্চতা। কাজেই কোনো ঘনবস্তুকে বলা যায় একটি ‘ত্রিমাত্রিক বস্তু’ (Three Dimensional or 3D Object), কারণ এর তিনটি মাত্রা রয়েছে। হিসেবের খাতিরে ধরা যাক, এখানে তিনি যে ঘনবস্তুর উপর শুয়ে আছেন তার দৈর্ঘ্য ৩ মিটার, প্রস্থ ২ মিটার এবং উচ্চতা ২ মিটার। অতএব,

আয়তন = ৩ মিটার X ২ মিটার X ২ মিটার = ১২ ঘনমিটার

৬৩৭ নিউটন / ১২ ঘনমিটার = ৫৩.০৮ নিউটন/মিটার^(^৩)

সাধারণত, কনক্রিট বা রডের ওজন এ ধরনের এককে প্রকাশ করা হয়ে থাকে। যেমনঃ পাথর ব্যবহার করে তৈরি করা ‘রিইনফোর্সড কনক্রিট’ এর ওজন ধরা হয় ২৫ কিলোনিউটন/মিটার^(^৩) (সূত্রঃ অনুচ্ছেদ ২.২.৪, ছক ৬.২.১, বিএনবিসি ২০২০)।

সমবণ্টিত ভারকে শুধুমাত্র এককের ভিত্তিতে আলাদা করে চিন্তা না করে আরো একভাবে তা করা যায়। মনে হয়তো প্রশ্ন আসতে পারে, আমাদের শরীরের সব জায়গার ওজন তো সমান না। এই যেমন, দুই হাতের ওজনের চেয়ে আমাদের দুই পায়ের ওজন বেশি হবে। আবার হাতের চেয়ে আমাদের মাথার ওজন কম হবে। এভাবে বিভিন্ন অঙ্গ-প্রত্যঙ্গের বিভিন্ন ওজন হয়। ঐ ব্যক্তি যখন মাটির উপর শুয়ে ছিলেন তখন তার সমস্ত অঙ্গ-প্রত্যঙ্গ থেকে তো সমান ভার মাটিতে যায়নি, হাত এক ধরনের ভার দিয়েছে, পা একরকম, আবার মাথা আরেকরকম ভার বা ওজন দিয়েছে। প্রতিটি ওজনের মান আলাদা।

তাহলে আমরা সমবণ্টিত ভার হিসেবের সময় যে পুরো শরীর জুড়ে একইভাবে আমাদের পুরো ভার বণ্টন করে দিলাম, তা কি ঠিক হলো? ব্যাপারটা হয়ে গেছে পুরো ঐকিক নিয়মের গণিতের মতো, যদি ৫ জন শ্রমিক মোট ২৫ টাকা পায়, তাহলে ১ জন শ্রমিক কত টাকা পাবেন? ঐকিক নিয়ম অনুযায়ী, ২৫/৫ = ৫ টাকা করে প্রতি জন শ্রমিক পাবেন। বাস্তবে হিসেবটা অতো সহজ নাও হতে পারে। এমনও তো হতে পারে, একজন পেয়েছেন ১০ টাকা, অন্যজন ৬ টাকা, বাকি তিনজন প্রত্যেকে ৩ টাকা করে। এছাড়াও আরো নানাভাবে বণ্টন হতে পারে। সবসময় যে সমানভাবে বণ্টন করা যাবে ব্যাপারটা এমন নয়। তাহলে কখন সমানভাবে ভার বণ্টন করা যুক্তিসঙ্গত হবে আর কখন হবে না, তা বোঝা বেশ জরুরি।

যদি এমন হতো আমাদের শরীরের প্রতিটি অঙ্গ একই পরিমাণের ওজন দেয় তাহলে কিন্তু ঐ ঐকিক নিয়মে ভার বণ্টন সঠিকই ছিল। একেক অঙ্গ একেক পরিমাণের ভার দেয় বলেই ঝামেলা বেঁধেছে। তবে পুরকৌশলীদের একটা সুবিধা হলো, দালানে ব্যবহৃত বিভিন্ন অংশ সাধারণত সুষম হয়। একটি কলামের দিকে তাকালে দেখা যাবে, সাধারণত এর আগাপাছতলা একেবারে সমান মাপের ও সুষম হয়। বিম ও স্ল্যাবের ক্ষেত্রেও তাই, ভেতরে যে রড ব্যবহার করা হয় তাও সুষম আকারের হয়ে থাকে। কাজেই তাদের ক্ষেত্রে সমবণ্টিত ভরের ধারণা গাণিতিকভাবে সঠিক হিসেবে ধরা যায়, এতে কোনো সমস্যা নেই (*নোটঃ এটা না হলে পুরকৌশলের গাণিতিক হিসাব আরো বেশি জটিল হতো, তখন হয়তো বিংশ শতাব্দীতে আমরা হার্ডিঞ্জ সেতুর মতো জটিল স্থাপনা নির্মিত হতে দেখতাম না)।

তবে কিছু কিছু এমন স্থাপনা বা তার অংশ আছে যেখানে আসলেই সমভাবে ভার বণ্টন করা গাণিতিকভাবে ভুল হবে। যেমনঃ এমন কিছু ভার আছে যেখানে বস্তুর এক প্রান্তে একেবারে শূন্য ভার থাকে, আর অন্যপ্রান্তে যেতে যেতে ভারের মান আস্তে আস্তে সমানভাবে বাড়তে থাকে।

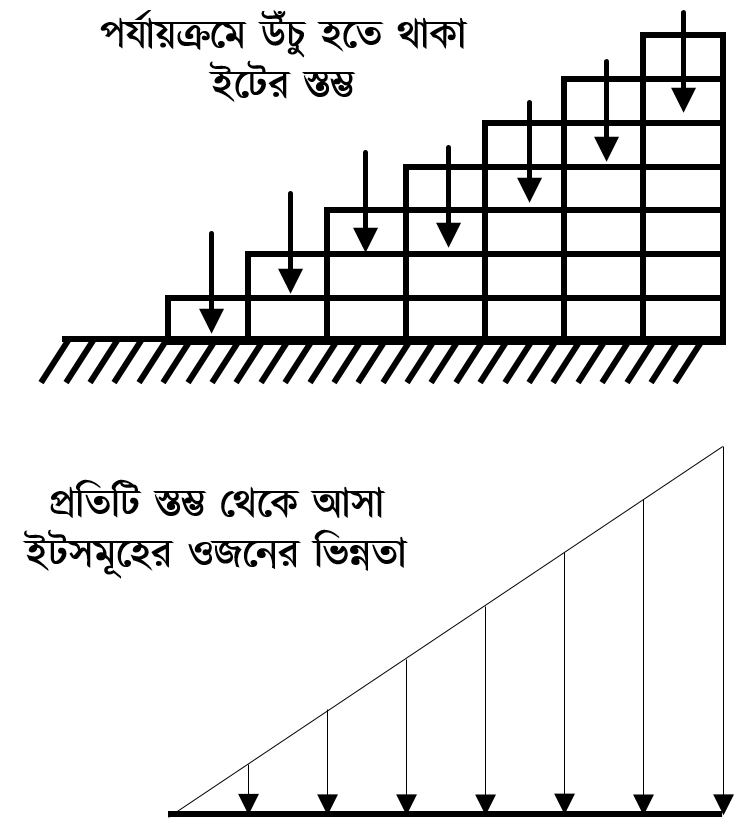
ধরি, মাটির উপর সারি করে ইট রাখা আছে, তবে তা বিভিন্ন সংখ্যায়। প্রথম সারিতে কোনো ইট নেই, দ্বিতীয় সারিতে একটি ইট, তৃতীয় সারিতে দুইটি, চতুর্থ সারিতে তিনটি, পঞ্চম সারিতে চারটি ও ষষ্ঠ সারিতে পাঁচটি ইট রয়েছে। অর্থাৎ ইটগুলো যে মাটির উপর রাখা হয়েছে তার একপ্রান্ত থেকে অন্যপ্রান্তে ওজনের মান ধীরে ধীরে সমানভাবে বাড়তে থাকে। প্রথম সারিতে সবচেয়ে কম ওজন কারণ সেখানে কোনো ইট নেই। আর ষষ্ঠ সারিতে ওজন সবচেয়ে বেশি। এ ধরনের ওজনকে বলা হয়, ‘সমভাবে পরিবর্তিত ভার’ (Uniformly Varying Load, UVL)। ভারের এক প্রান্তে শূন্য থেকে অন্যপ্রান্তে সর্বোচ্চ মানে পৌঁছায় বলে এ ভারকে দেখতে অনেকটা ত্রিভুজের মতো দেখায়। তাই একে ‘ত্রিভুজাকৃতির ভার’ বা Triangular Load বলে।

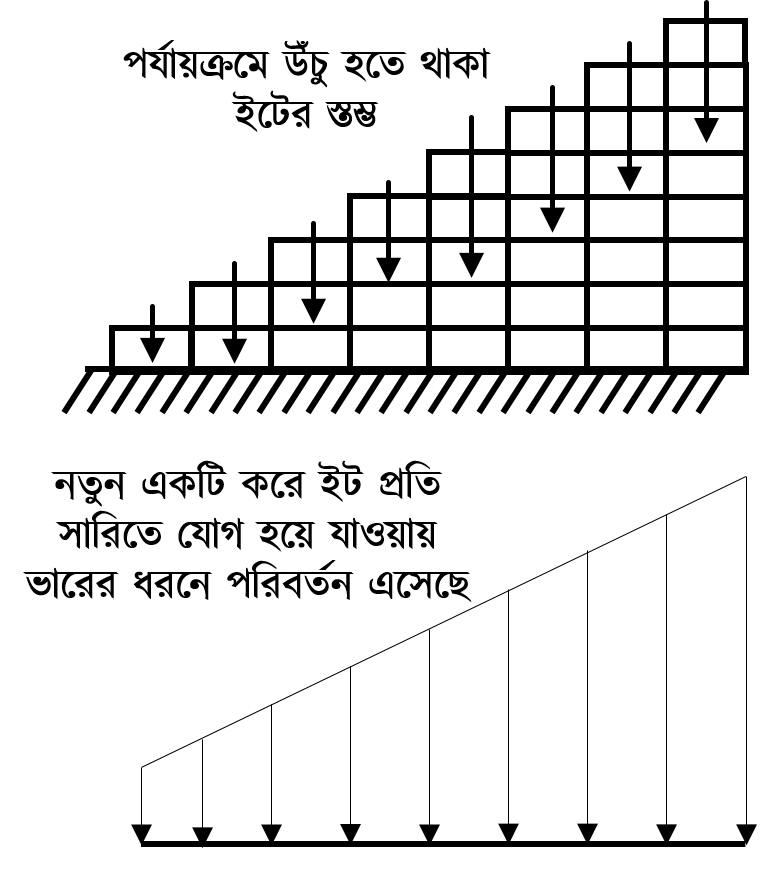
এখন ধরা যাক যে প্রথম সারিতে কোনো ইট রাখা ছিল না সেখানে একটি ইট রেখে দেওয়া হলো, এবং একইভাবে বাকি প্রতি সারিতে একটি করে ইট বাড়িয়ে দেয়া হলো। এখন কিন্তু আর ভারের মান এক প্রান্তে শূন্য থেকে শুরু হবে না, সেখানে একটি ইটের ওজনের সমান ভার থাকবে, যা বাড়তে বাড়তে ষষ্ঠ সারিতে ছয়টি ইটের সমান ওজনে গিয়ে ঠেকবে। এ ধরনের ভারকে লেখচিত্রে দেখতে অনেকটা ট্র্যাপিজয়েডের মতো দেখায় বলে একে ‘ট্র্যাপিজয়ডাল ভার’ (Trapezoidal Load) বলে। সবমিলিয়ে সারমর্ম করলে দাঁড়ায়, সমভাবে পরিবর্তিত ভার দুই প্রকারের হতে পারে- ১. ত্রিভুজাকৃতির ভার, এবং ২. ট্র্যাপিজয়ডাল ভার।

সমবণ্টিত ভারকে আরেকভাবে চিন্তা করা যায়। একটু গভীরে ঢুকলে দেখা যাবে, যদি কোনো বস্তুর সম্পূর্ণ ভারকে একটি বিন্দুতে নিয়ে আসা যেতো তাহলে কী হতো? প্রথমে একটু গাণিতিকভাবে ব্যাখ্যা দেয়া যাক। এ আলোচনায়, দৈর্ঘ্যের ভিত্তিতে সমবণ্টিত ভার ৩১৮.৫ নিউটন/মিটার এবং ব্যক্তির উচ্চতা ২ মিটার। তাহলে পুরো ওজনকে একটি বিন্দুর উপর কাজ করছে ধরে নিলে সেই ওজনের মান হবে, ৩১৮.৫ নিউটন/মিটার X ২ মিটার = ৬৩৭ নিউটন। 

এখন ৬৩৭ নিউটন বল পুরো বস্তু জুড়ে কাজ করছে বলে চিন্তা করা হবে না, চিন্তা করতে হবে এই বল বস্তুর নির্দিষ্ট একটি বিন্দুতে কাজ করছে। এভাবে যখন সমবণ্টিত ভারকে একটি নির্দিষ্ট বিন্দুতে কেন্দ্রীভূত করে চিন্তা করা হয়, এ ধরনের ভারকে বলে ‘ঘনীভূত ভার’ (Concentrated Load)। সাধারণত পুরো বস্তুর ওজন যে একটি নির্দিষ্ট বিন্দুতে কাজ করছে বলে বিবেচনা করা হয়, তাকে বলে ‘অভিকর্ষ কেন্দ্র’ (Centre of Gravity)।

ব্যবহারের ভিত্তিতে ভারের ধরন

দালানের ভেতর এমন কিছু জিনিস থাকে যা দালানের জীবনকালে সর্বদা দালানের সাথে জুড়ে থাকবে। দালানের কলাম, বিম, স্ল্যাব প্রভৃতি স্থায়ী অংশকে চিন্তার বাইরে রেখে কখনো দালানের অস্তিত্ব কল্পনা করা যাবে না। দালানের এ স্থায়ী অংশগুলো থেকে যে ভার আসে তাকে বলা হয় ‘স্থায়ী ভার’ বা Dead Load। দালানের ভেতরে রাখা বিভিন্ন আসবাবপত্র যা কখনো এক জায়গা থেকে অন্য জায়গায় সরানো হবে না বা সরানো সম্ভব নয়, তাদের ভারও স্থায়ী ভারের ভেতর অন্তর্ভুক্ত হবে। দালানের কাঠামোগত অংশের ভেতর পড়ে না কিন্তু স্থায়ীভাবে তা দালানের অংশ হয়ে আজীবন থাকবে, এদের ভারও স্থায়ী ভার, যেমনঃ বিভাজক দেয়াল (Partition Wall), মেঝেতে বসানো টাইলস, দরজা, জানালা, সানশেড, প্রভৃতির ভার।

দালানের ভেতরে থাকা যেকোনো জিনিস যা এক স্থান থেকে অন্য স্থানে সরিয়ে ফেলা সম্ভব, বা এক সময় তা হয়তো দালানে আর কোনো দিন নাও থাকতে পারে, এমন ধরনের বস্তু থেকে আসা ভারকে বলা হয় ‘অস্থায়ী ভার’ (Live Load)। দালানের ভেতরে থাকা মানুষের ভার, আসবাবপত্রের ভার, বিভিন্ন ইলেক্ট্রনিক যন্ত্রপাতির ভার, প্রভৃতি অস্থায়ী ভারের অন্তর্ভুক্ত। দালানের কোন কোন অংশ থেকে কী ধরনের ভার আসতে পারে তা বাংলাদেশ জাতীয় ইমারত বিধিমালা (বিএনবিসি), ২০২০ তে নির্দিষ্টভাবে উল্লেখ করা আছে। 

(এরপর দেখুন ৪র্থ পর্বে)

আগের পর্ব-

পুরকৌশলের প্রাথমিক ধারণা || পর্ব ১ || বেঁচে থাকার জন্য বাসস্থান কেন জরুরি?
পুরকৌশলের প্রাথমিক ধারণা || পর্ব ২ || জেলখানা আর মসজিদের মধ্যে তফাতটা কেন বলে দিতে হয় না?