আপনি এখন যে কম্পিউটার বা স্মার্টফোনে এই লেখাটি পড়ছেন, সেটি সম্ভব হয়েছে ০ এবং ১ এর জন্য, অর্থাৎ বাইনারি নাম্বার সিস্টেমের সূত্র ধরে আপনি এই লেখাটি পড়ছেন। বাইনারি নাম্বার সিস্টেমের অবিচ্ছেদ্য একটি সংখ্যা হচ্ছে শূন্য (০)। এটি না থাকলে বাইনারি নাম্বার সিস্টেম থাকতো না। আধুনিক ইলেক্ট্রনিক্সের অস্তিত্বই থাকতো না, যদি শূন্য আবিষ্কার না হতো! শূন্য আবিষ্কার না হলে ক্যালকুলাস থাকতো না। এর মানে এই যে, অটোমেশন-ইঞ্জিনিয়ারিং তারও কোনো অস্তিত্ব থাকতো না। শূন্য বিনা আমাদের এই আধুনিক পৃথিবী কল্পনা করাও খুব দুষ্কর।

মানব ইতিহাসে শূন্যের আবিষ্কার আধুনিকায়নের পথকে বাজিমাত করে দিয়েছে। শূন্য শুধুমাত্র একটি অংক বা সংখ্যা নয়। শূন্যকে বুঝতে পারা একটি দ্বিতীয় ভাষা শেখার মতোই বলে তুলনা করা হয়। কারণ এই শূন্য একদিনে বা জন্মের সাথে সাথে মানুষ আত্মস্থ করতে পারেনি। শূন্যের ধারণা আমাদের সহজাত কোনো বিষয় না। মনুষ্য সম্প্রদায়কে এই শূন্য আবিষ্কার ও গবেষণা করতে হয়েছে। আধুনিকায়নের পথ সুগম রাখার জন্যই পরবর্তী প্রজন্মের কাছে এই শূন্যকে প্রসারিত করে যেতে হবে।
মানুষ ছাড়া প্রাণীজগতের অন্যান্য প্রানী, যেমন- বানর শূন্যের একটি অসম্পূর্ণ ধারণা নিজেদের মধ্যে গঠন করতে পারে। এমনকি বিজ্ঞানীরা বলছেন, ক্ষুদ্র মৌমাছিও শূন্য গণনা করতে পারে! কিন্তু পৃথিবীতে একমাত্র মানুষই শূন্যকে আবিষ্কার করতে পেরেছে এবং একে জব্দ করে, বিভিন্ন কর্ম হাসিলের মাধ্যম হিসেবে ব্যবহার করতে পেরেছে।
তাই শূন্যকে শূন্য বলে ছোট করবেন না। শূন্যের অবদান অসীমেরও বেশি! চলুন তাহলে একটু শূন্যের গভীরে যাওয়া যাক!
যা-ই হোক শূন্য আসলে কী?
প্রকৃতি শূন্যস্থান পছন্দ করে না- এই প্রবাদ বাক্যটি মেনে নিলে শূন্য সম্পর্কে গভীর ধারণা পাওয়া সম্ভব। অন্যভাবে বলতে গেলে, আমরা প্রকৃতিতে তেমন একটা শূন্যের সম্মুখীন হই না।
১, ২, ৩… এই অঙ্কগুলোর প্রতিটিরই কোনো না কোনো প্রতিরূপ আপনি তৈরি করতে পারবেন। যেমন- একটি বাতি জ্বলতে দেখি, দুটো পাখি উড়ে যায়, টেবিলে তিনটি বই। কিন্তু শূন্য? শূন্য সংখ্যক কোনো বস্তু কি দেখেছেন? অর্থাৎ শূন্যকে বুঝতে হলে আমাদের আগে বুঝতে হবে, যেকোনো কিছুর অনুপস্থিতি বা অবর্তমান নিজেই এমন একটি ব্যাপার, যার অস্তিত্ব আছে!
হার্ভার্ডের গণিতের অধ্যাপক এবং শূন্য নিয়ে লেখা একটি বইয়ের লেখক রবার্ট কাপলান বলেন, শূন্যের অস্তিত্ব বিরাজ করে মনের মধ্যে। শূন্য এই সংবেদী জগতের মধ্যে দৃশ্যমান নয়। আপনি অসীম, খালি আকাশের দিকে তাকালেও যদি একটি তারা দেখতে পান, তার মানে ঐ অসীম আকাশও শূন্য নয়। কিছু না কিছু সবসময়ই আছে। ধ্রুবতম শূন্য যদি কিছু থেকে থাকে, তাহলে সেটি হয়তো বিগ ব্যাংয়ের পূর্বে কখনো ছিল, কিন্তু আমরা তা সঠিকভাবে জানি না। শূন্যের সাপেক্ষে অন্যান্য সংখ্যা গণনার সহজ পদ্ধতি সাজিয়েছিলেন জন ভন নিউম্যান।

শূন্যকে অনুধাবন বা শূন্যকে ব্যবহার করতে হলে শূন্যের প্রকাশ্য অবস্থায় থাকার দরকারও নেই। বরং শূন্যের ধারণাকে কেন্দ্র করে আমরা মহাবিশ্বের অন্যান্য সংখ্যা গণনা করতে পারি।
ধরুন, একটি খালি বাক্স আছে, যার ভেতর কিছুই নেই। এই খালি বাক্সের ভেতর যেহেতু কিছুই নেই, তাই এটি শূন্যের একটি কল্পিত প্রতিরূপ। বিজ্ঞানীরা একে খালি সেট বলে থাকেন। এখন আরেকটি খালি বাক্স নিন। এই খালি বাক্সটি প্রথম খালি বাক্সের ভেতর রাখুন। এবার বলুন, প্রথম খালি বাক্সের ভেতর কয়টি জিনিস আছে? উত্তর হচ্ছে, একটি। এবার আরো একটি খালি বাক্স নিয়ে এই দুটি খালি বাক্সের ভেতর রাখুন। এখন প্রথম খালি বাক্সটিতে কয়টি জিনিস আছে? দুটি। এভাবেই আমরা শূন্য থেকে অন্যান্য সংখ্যা নিরূপণ করতে পারি। এভাবেই শূন্য থেকেই আমরা অংক বা সংখ্যা নির্ণয় করে থাকি। এটাই আমাদের নাম্বার পদ্ধতির মূল ভিত্তি। শূন্য একইসাথে বাস্তব এবং বিভ্রান্তিকর!

যখন শূন্যকে আবিষ্কার করা গেল, তারপর পাওয়া গেল ঋণাত্মক সংখ্যা! শূন্যের সাহায্যে আমরা এমন কিছু ব্যাপার বুঝতে পারি, যার কোনো অস্তিত্ব হয়তো বাস্তব জীবনে নেই! ইমাজিনারি নাম্বার বা কাল্পনিক সংখ্যার কোনো অস্তিত্ব কিন্তু মানবজীবনে নেই, কিন্তু তা-ও এটি জটিল ইলেকট্রিক্যাল সিস্টেম গঠন এবং বোঝার জন্য খুব গুরুত্বপূর্ণ ব্যাপার। শুধু তা-ই নয়, শূন্যের জন্য আমরা বৈপরীত্য, অসীমতা এবং আরো অদ্ভুত কিছু ব্যাপার অনুধাবন করতে পারি।
গণিতে কেন শূন্য এত দরকারি!
গণিতে শূন্যের প্রভাব দু’রকম। প্রথমত, এটি সংখ্যাতত্ত্বের একটি গুরুত্বপূর্ণ স্থান-ধারণকারী (প্লেসহোল্ডার) সংখ্যা এবং দ্বিতীয়ত, শূন্য তার নিজের অবস্থানে নিজের অধিকারে সমুন্নত।
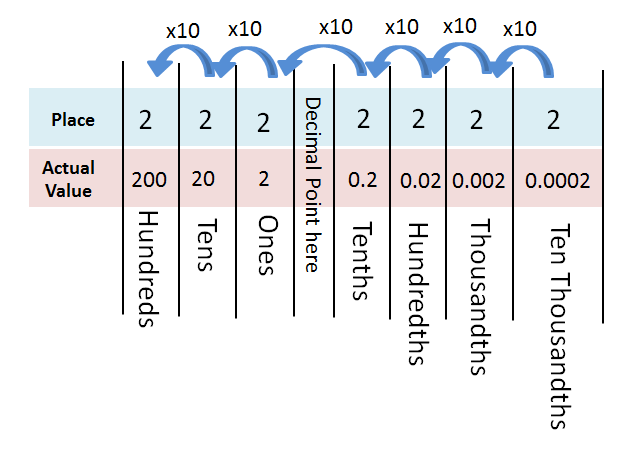
মানব ইতিহাস পর্যালোচনা করলে দেখা যায়, আজ থেকে পাঁচ হাজার বছর আগে মেসোপটেমিয়া অঞ্চলে সর্বপ্রথম শূন্যের ব্যবহার প্রচলিত হয়েছিল। কোনো সংখ্যার মধ্যে একটি অঙ্কের অনুপস্থিতি প্রকাশ করতে শূন্য ব্যবহার করা হতো। উদাহরণস্বরূপ ধরুন, আপনার কাছে ১০৩টি আপেল আছে। এখন ১ এবং ৩ এর মাধ্যমে একশত তিন লিখা দুরূহ। কারণ ১ এবং ৩ মিলিয়ে ৩১ এবং ১৩ ছাড়া আর কোনো সংখ্যা গঠন করা যাচ্ছিলো না। ফলে ১০৩ লিখে এখানে ১ এবং ৩ এর মাঝে শূন্য ব্যবহার করে বোঝানো হয়েছে দশমিকের ঘরে কিছুই নেই। অর্থাৎ ১ এবং ৩ এর মাঝে শূন্য থাকার ফলে আমরা বুঝতে পারি, এই সংখ্যাটি একশ তিন, তেরো না।
শূন্য যে শুধুমাত্র নাম্বার সিস্টেমের একটি স্থান-ধারণকারী কিছু নয়, এর বাইরেও শূন্য যে আসলেই শূন্য- এই তত্ত্বের প্রথম ব্যাখ্যা পাওয়া যায় ভারতে। আজ থেকে দেড় হাজার বছর বা তারও পূর্বে। মধ্য আমেরিকার প্রাচীন মায়ানরাও তাদের সংখ্যা পদ্ধতিতে শূন্যের ব্যবহার শুরু করেছিল।
সপ্তম শতাব্দীতে ভারতের গণিতবিদ ব্রহ্মগুপ্ত সর্বপ্রথম শূন্যের লিখিত বিবরণ লিপিবদ্ধ করেন। তিনি লিখেছিলেন, কোনো সংখ্যার সাথে শূন্য যোগ বা বিয়োগ করলে সেই সংখ্যার কোনো পরিবর্তন হয় না। আবার কোনো সংখ্যার সাথে শূন্য গুণ করলে সেটিও শূন্য হয়ে যায়! আর ভাগ করলে তার মান গিয়ে দাঁড়ায় অসংজ্ঞায়িত!

ভারত থেকে শূন্যের এই ধারণা ইউরোপে পৌঁছাবার আগে মধ্যপ্রাচ্যেও ছড়িয়ে পড়ে। ১২ দশকের দিকে গণিতবিদ ফিবোনেচি আরবি সংখ্যা পদ্ধতিকে জনপ্রিয় করে তুলেছিলেন। সেই থেকে শুরু করে এযাবতকালে আমরাও এই শূন্যের ব্যবহার করেই যাচ্ছি। শুধুমাত্র গণনা এবং সংখ্যা পদ্ধতি না, বিজ্ঞানেও শূন্যের অবদান অপরিসীম!
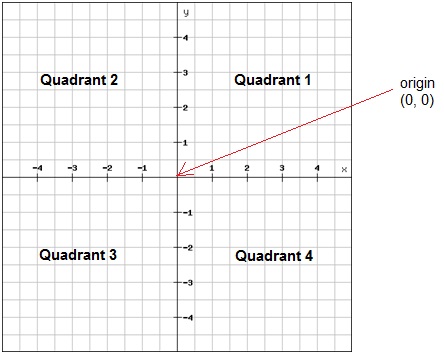
এভাবেই গণিতে শূন্যের প্রচলন বাড়তে থাকে। (০, ০) মূলবিন্দু বিশিষ্ট একটি লেখচিত্র বা গ্রাফের কথা চিন্তা করুন তো! সতেরো শতাব্দীতে ইউরোপে শূন্যের ধারণা পৌঁছাবার পরই এই মূলবিন্দু বিশিষ্ট লেখচিত্র বা গ্রাফ আবিষ্কৃত হয়েছিল। আর এ থেকেই বা বলতে গেলে শূন্যের উপর নির্ভর করেই গণিতের নতুন একটি ক্ষেত্র আবিষ্কৃত হয়, যার নাম ক্যালকুলাস! ক্যালকুলাস আছে বলেই আজ ইঞ্জিনিয়ারিং ক্ষেত্রটি এত সমৃদ্ধ এবং আধুনিক।
শূন্য কেন মনুষ্য ধারণা থেকে বিকশিত?
আমরা জন্মের পরপরই শূন্য সম্পর্কে সঠিকভাবে বুঝতে পারি না। সময়ের সাথে সাথে আমাদের শূন্যকে বুঝে নিতে হয়, শিখে নিতে হয়। মানুষ এবং অন্যান্য প্রাণীরা সংখাকে কীভাবে তাদের মনে উপস্থাপিত করে এ বিষয়ে গবেষণা করছেন ডিউক ইউনিভার্সিটির নিউরোসায়েন্টিস্ট এলিজাবেথ ব্র্যানন।
তিনি বলেন, ৬ বছর বয়সের যেকোনো বাচ্চাই শূন্য বলতে বুঝে থাকে ‘কিছুই না’। যদিও তখন তারা গণিতের অন্তর্নিহিত বিষয়বস্তু ভালভাবে বুঝতে পারে না বা একেবারেই বোঝে না। কিন্তু তাদেরকে যদি জিজ্ঞাসা করা হয় ১ এবং ০ এর মধ্যে কোনটি সবচাইতে ছোট, তখন তারা ভাবনায় পড়ে যায় সঠিক উত্তর কোনটা হবে! এবং বেশিরভাগ সময়ই মনে করে ১ সবচাইতে ছোট সংখ্যা। ব্র্যানন বলেন, শূন্য যে ১ এর থেকে ছোট এটা বুঝতে তাদের বেশ সময় লাগে যায়।
ব্র্যানন প্রায়শই ৪ বছর বয়সী বাচ্চাদের সাথে একটি পরীক্ষামূলক খেলা খেলে থাকেন। পরীক্ষাটিতে দুটি কার্ডের ব্যবহার করা হয়ে থাকে এবং প্রতিটি কার্ডের উপর একটি নির্দিষ্ট সংখ্যক বস্তু রাখা বা আঁকা হয়। ধরা যাক একটি কার্ডের উপর দুটি ডট চিহ্ন, অপর একটি কার্ডের উপর চারটি ডট চিহ্ন আঁকা হয়েছে।
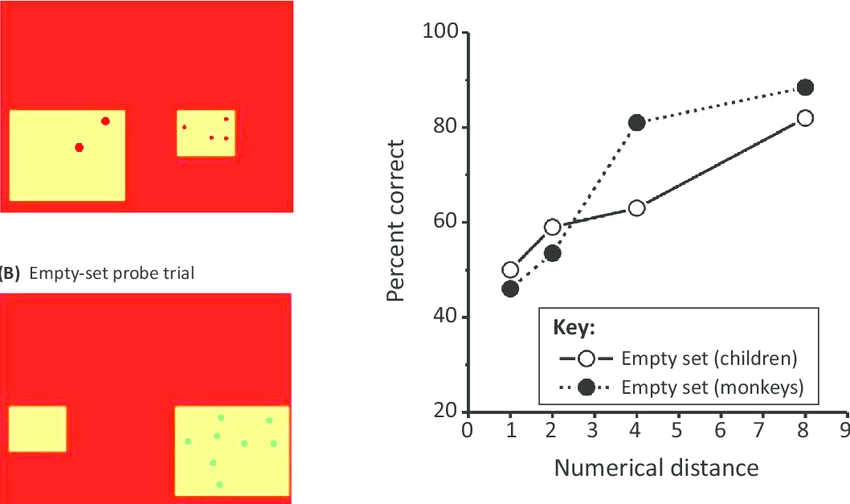
এবার তিনি বাচ্চাদেরকে সবচাইতে কম ডট আঁকা কার্ডটি বাছাই করতে বলেন। এক্ষেত্রে তারা সহজেই কম সংখ্যক ডট আঁকা কার্ড বাছাই করতে পারে। কিন্তু এই খেলায় যখন কোনো কার্ডের উপর কোনো ডট আঁকা থাকে না, অর্থাৎ একটি খালি কার্ড এবং আরেকটি ডট আঁকা কার্ড দেয়া হয়, তখন অর্ধেকের কম সংখ্যক বাচ্চা সঠিক উত্তর দিতে পারে। অর্থাৎ অর্ধেকের কম বাচ্চা খালি কার্ডকে সবচাইতে কম সংখ্যক ডটযুক্ত কার্ড হিসেবে চিহ্নিত করতে পারে।
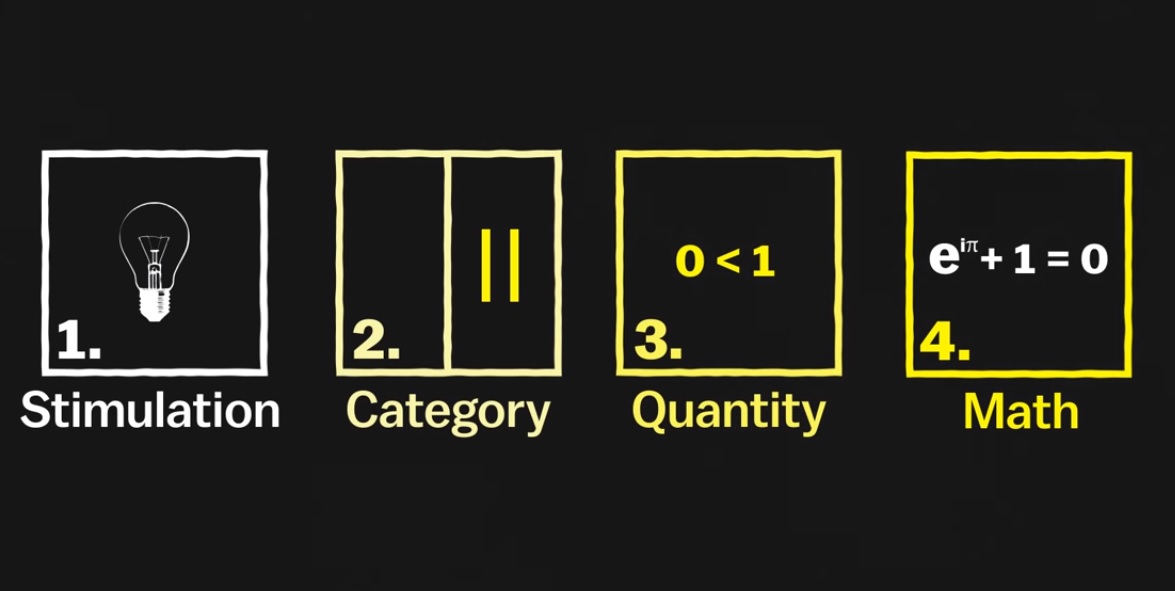
জার্মান গণিতবিদ আন্দ্রেস নিদার মনে করেন, শূন্যকে বোঝার জন্য চারটি মনস্তাত্ত্বিক ধাপ পার হতে হয়। প্রতিটি ধাপ তার পূর্বের পদক্ষেপ থেকে খানিকটা জটিল। নিদার মনে করেন, চারটি ধাপের প্রথম তিনটি ধাপ অনেক প্রাণীই অতিক্রম করতে পারে, কিন্তু চতুর্থ ধাপটি কেবল মানুষের পক্ষেই পার করা সম্ভব, বা মানুষের জন্য সংরক্ষিত।
প্রথম ধাপ হচ্ছে কোনো কিছুর অস্তিত আছে নাকি নেই সেটি টের পাওয়া। যেমন- একটি আলো বা সংবেদী কোনো কিছুর অস্তিত্ব প্রকাশ পেয়ে আবার মিলিয়ে গেলো, অর্থাৎ কয়েকটি লাইট জ্বলে আবার বন্ধ হয়ে যাওয়া বা কোনো শব্দ সৃষ্টি হয়ে আবার বন্ধ হয়ে যাওয়া।
দ্বিতীয় ধাপ হচ্ছে এই কিছু আছে বা কিছু নেই এর উপর আচরণগত ব্যবহার। এই ধাপে প্রাণী কেবল উদ্দীপনার অস্তিত্ব বা অনুপস্থিতিকে টেরই পায় না, এর প্রভাবে প্রতিক্রিয়াও জানাতে পারে। যেমন- কারো ঘরে যদি খাবার শেষ হয়ে যায় বা খাবার না থাকে, তখন সে আরো খাদ্য সংগ্রহের চেষ্টা করে। অর্থাৎ শূন্যতা টের পেয়ে সেই শূন্যতাকে মেটাবার প্রয়াস চালায়।
তৃতীয় ধাপ হচ্ছে শূন্যকে বুঝতে বা চিনতে পারা। কোনো কিছু নেই, বা খালি একটি ধারককে শূন্য হিসেবে অভিহিত করা। ব্যাপারটি খুব কৌশলী হলেও বানর এবং মৌমাছি এই ধাপ পর্যন্ত পৌঁছাতে পারে। এটি এমন একটি ধাপ, যেখানে কোনো কিছুর না থাকাকে সাংখ্যিক মান দিয়ে তালিকাভুক্ত করা যায়।
চতুর্থ ধাপটি হচ্ছে সবচাইতে কঠিন। এটি কেবল মানুষের পক্ষেই অতিক্রম করা সম্ভব হয়েছে। কোনো প্রভাবক বা কোনো কিছুর অনুপস্থিতিকে খেয়াল করে, তাকে শূন্য বলে অভিহিত করে, শূন্যকে একটি চিহ্ন বা প্রতীক হিসেবে ব্যবহার করা। মানুষ ছাড়া অন্যান্য যেকোনো প্রাণী যতই স্মার্ট হোক না কেন, শূন্য যে একটি সাংখ্যিক চিহ্ন হতে পারে- এটি কেবল মানুষই বুঝতে পারে। এমনকি কখনো কখনো মানুষও শূন্যকে নিয়ে ভাবতে গেলে একটু কিংকর্তব্যবিমূঢ় হয়ে যেতে পারে।
ব্র্যাননের কম ডট চিহ্নিত কার্ড বাছাইয়ের খেলা যখন বড়দের সাথে খেলা হয়, তখন শূন্য থেকে বড় সংখ্যার তুলনায় শূন্য এবং একের মধ্যে সিদ্ধান্ত নেয়ার সময় প্রাপ্তবয়স্ক মানুষ খানিকটা বেশি সময় নিয়ে থাকে। অর্থাৎ শূন্যকে সঠিকভাবে বোঝার জন্য আমাদের মস্তিষ্ককে একটু বেশি খাটতে হয়।
আর কোনো প্রাণী শূন্যকে বুঝতে পারে?
শূন্যকে পুরোপুরি বুঝবার এবং ব্যবহার করবার জন্য যে চারটি ধাপ আছে, তার মধ্যে চার নাম্বার ধাপটি কেবল মানুষই অতিক্রম করতে পারে। কিন্তু অবাক করার মতো বিষয় হলেও সত্য যে, বেশ কিছু প্রাণী তৃতীয় ধাপ পর্যন্ত যেতে পারে। অর্থাৎ তারা বুঝতে পারে, একের চেয়ে শূন্য ছোট!
রয়াল মেলবোর্ন ইনস্টিটিউটের পিএইচডি শিক্ষার্থী স্কারলেট হাওয়ার্ড একটি গবেষণা প্রবন্ধ প্রকাশ করেছেন, যে গবেষণায় তিনি ব্র্যাননের করা পরীক্ষাটি অবিকলভাবে মৌমাছির সাথে করেছেন। প্রায় ৬০-৭০ শতাংশ ফলাফলে মৌমাছি খালি কার্ডটি চিহ্নিত করতে সক্ষম হয়েছে। শূন্যের সাথে অন্য সংখ্যার ব্যবধান যত বাড়ানো হয়েছে, ফলাফল ততই ভাল হয়েছে।
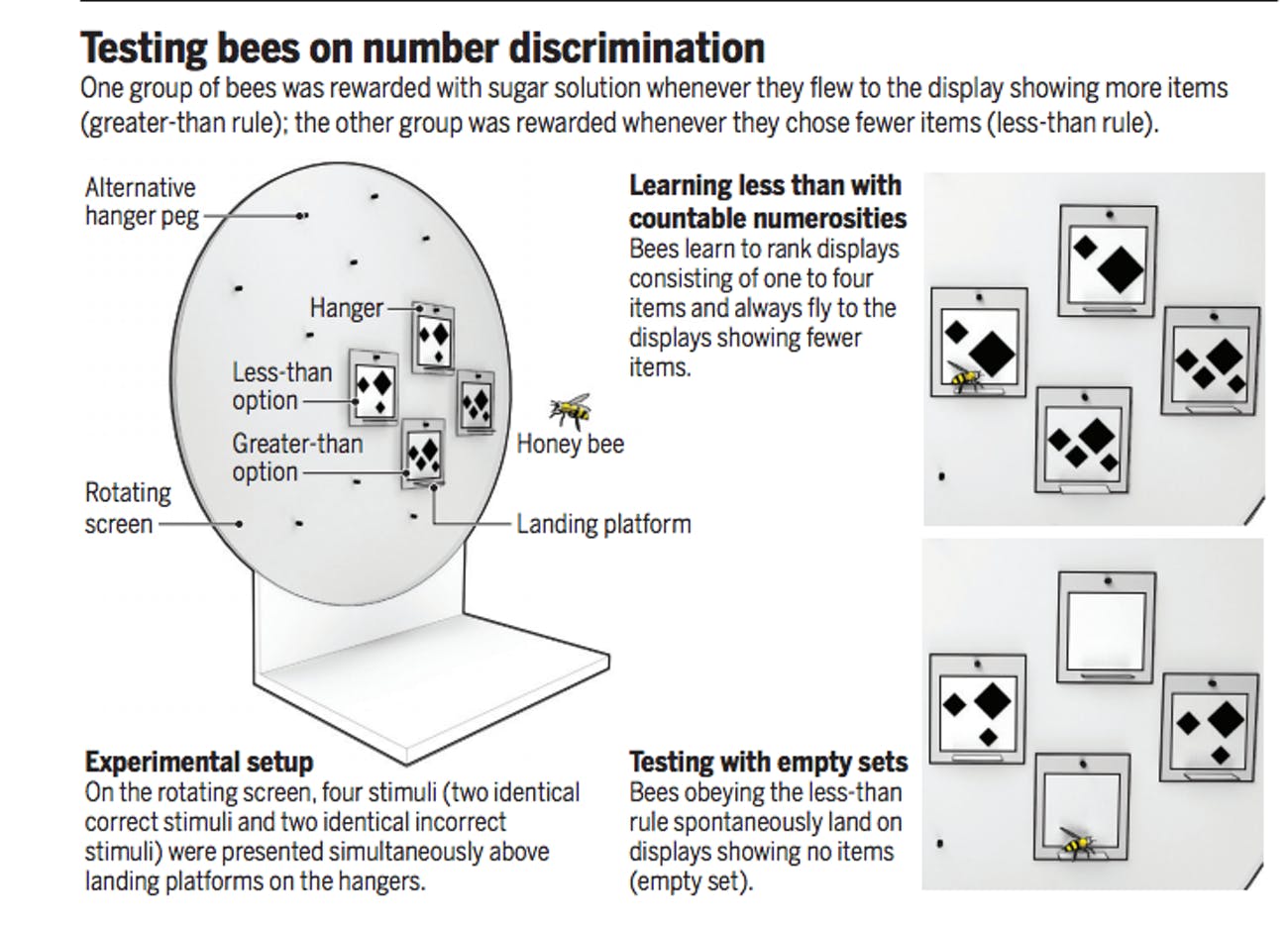
হাওয়ার্ড মনে করেন, তার গবেষণা দল অচিরেই মৌমাছিদের মস্তিস্কে গণনা পদ্ধতি কীভাবে কাজ করে তা আবিষ্কার করতে পারবে, এবং সেই পদ্ধতি অনুসরণ করে আরো প্রযুক্তিগত সমৃদ্ধ কম্পিউটার তৈরি করা সম্ভব হবে।
তিনি মনে করেন, শূন্য এখনো একটি বিশাল রহস্য। একে আবিষ্কারের আরো অবকাশ রয়েছে। আন্দ্রেস নিদার বলেন,
“শূন্য সম্পর্কে খুব কমই আমরা এখন পর্যন্ত আবিষ্কার করতে পেরেছি। এবং আমাদের মস্তিষ্ক কীভাবে শূন্যকে বিবেচনা করে তা-ও আমরা খুব একটা জানি না। মানুষ, বানর এবং মৌমাছি ছাড়া আর কত প্রজাতির প্রাণী এই শূন্য বা শূন্যতাকে বুঝতে পারে তা-ও আমাদের জানার বাইরে।”
কিন্তু শূন্য নিয়ে গবেষণা করে বিজ্ঞানীরা আমাদের দেখিয়েছেন, শূন্য নিয়ে গবেষণা বা তদন্ত করতে গেলে আমরা কিছু না কিছু পাবোই পাবো!








