
ක්රිස්තු පූර්ව 600 දී පමණ ජීවත් වූ ක්රීට ජාතික දාර්ශනිකයෙකු වූ එපිමෙනිඩස් මෙසේ පවසා ඇත. ‘සියළු ම ක්රීටයෝ බොරුකාරයෝ ය’

(yelp.com)
බැලූ බැල්මට මෙය වචනාර්ථයෙන් පැවසෙන දෙයින් අවසන් වන හුදු ප්රකාශයක් ලෙස පෙනිය හැක. එහෙත් එය එසේ නොවේ. මන්ද එපිමෙනිඩස් ද ක්රීටයෙකු වන බැවිනි. සියළු ම ක්රීටයෝ බොරුකාරයන් වනවා නම් එපිමෙනිඩස් ද බොරුකාරයෙකු විය යුතු ය. එසේ නම් ඔහුගේ ප්රකාශය ‘සියළු ම ක්රීටයෝ බොරුකාරයෝ ය’ යන ප්රකාශය ද බොරුවක් විය යුතු ය.
සියළු ම ක්රිටයෝ බොරුකාරයෝ ය යන්න බොරුවක් නම් සියළු ම ක්රීටයෝ බොරුකාරයන් විය නොහැක. එසේ නම් ඇත්ත කියන ක්රීටයෝ ද සිටිය යුතු ය. ඒ අනුව එපිමෙනිඩස් අයත් වන්නේ මෙම බොරු කියන ගොන්නට ය. ඔහුගේ ප්රකාශය බොරුවකි.
හොඳයි. අපි මේ කතා කරන්නේ විරුද්ධාභාස ගැන. විරුද්ධාභාස කියන්නෙ කුමක්ද යන ප්රශ්නයට ලිපිය මුල දී ම විසඳුමක් දෙනු වෙනුවට ඉදිරියේ දී හමුවන උදාහරණ ඔස්සේ ඔබට එය පැහැදිලි වේ යැයි අපි සිතමු. දර්ශනය තර්ක ශාස්ත්රය හෝ ගණිතය තරමක් ගැඹුරින් හදාරා නැත්නම් ඔබට මේවා පළමු බැල්මෙන් ජීර්ණය කරගත නොහැකි සේ දැනෙනු ඇත. ඇත්තට ම ඔබට එය එසේ දැනීම සාධාරණය. මොකද අප දන්නා ඉතිහාසය පුරා ම මේ සංකල්ප ඉතා ම නැවුම් විදියට කතිකාවට ගන්නට තරම් සිතන්නට යමක් ඉතිරි කල දේවල් නිසාත් එසේ වන්නට නම් ඒවා හිතන තරම් සරල නැති විය යුතු නිසාත් ය. පහතින් ඉදිරිපත් කරන ප්රශ්න ලේසියෙන් ග්රහණය කරගෙන ලේසියෙන් විසඳිය හැකි දේ නෙවෙයි. හැබැයි ඔබට විරුද්ධාභාස යන සංකල්පය වටහා ගන්නට තරම් මේ ලිපියේ වපසරිය ප්රමාණවත් වේවි. පහතින් නැගෙන්නට නියමිත ප්රශ්න වලට විසඳුම් ඔබ ම කල්පනා කර බලන්න.
එපිමෙනිඩස්ගේ ප්රකාශය ඇත්තට ම විරුද්ධාභාසයක් නෙවෙයි. ඒ ප්රකාශය බොරුවක්. මොකද එපිමෙනිඩස් බොරුකාරයෙකු නිසා. දැන් අපි ඒ ප්රශ්නය ම නියම විරුද්ධාභාසයකට හරවමු.
ඔබ ඔබේ පෙම්වතියට කියනවා.’මම බොරුකාරයෙක්’ කියල. ඒ ඇයට ලෝකෙ ම එපා වෙන මොහොත. ඒත් ඇය තර්කශාස්ත්රය හදාරා ඇති අයෙකු නම් ඇතිවන්නේ වෙනත් ආකාරයේ ප්රශනයක්. ඇය කල්පනා කරන්නේ මෙහෙමයි.
ඔබ මුලින් ම කරන ප්රකාශය ‘මම බොරුකාරයෙක්’ යන්නයි. ඔබ කියන්නේ ඇත්ත කියල හිතමු. දැන් ඔබ බොරුකාරයෙක්. ඒ කියන්නේ ඔබේ ප්රකාශ සියල්ල සාවද්යයයි. ඒ නිසා ‘මම බොරුකාරයෙක්’ යන ප්රකාශයත් බොරුවක් විය යුතු යි. එසේ නම්, ඔබ බොරුකාරයෙක් නොවේ, ඇත්ත කියන කෙනෙක්.
ඒ අනුව ඔබ ඇත්ත කියන කෙනෙක්.
ඒත් ප්රශ්නය එතැනින් අවසන් නෑ. මොකද ඔබ ඇත්ත කියන කෙනෙක් නම් ‘මම බොරුකාරයෙක්’ කියන ප්රකාශය ඇත්ත වෙන්න ඕනේ. ඒ කියන්නේ ඔබ බොරුකාරයෙක්. ඒත් පුද්ගලයෙක් ‘මම බොරුකාරයෙක්’ කියල ප්රකාශ කලොත් ඉන් අදහස් වෙන්නේ එම පුද්ගලයා බොරුකාරයෙකු නොවන බවයි, ඇත්ත කියන අයෙකු බවයි.
දැන් අපට ඉතිරිවන්නේ විසඳුමක් නැති ප්රශ්නයක්. සමහර ප්රකාශ සත්යයය වුණොත් අසත්යය වෙන්න ඕනේ. අසත්යය වුණොත් සත්යය වෙන්න ඕනේ. මේ වගේ ප්රකාශවලට තමා විරුද්ධාභාසී ප්රකාශ කියන්නේ.
පිනෝකියෝ විරුද්ධාභාසය

රහසේ බොරුවක් කියාගන්න බැරි පිනෝකියෝ (s712.photobucket.com)
මම බොරුකාරයෙක් විරුද්ධාභාසය තවත් අපූරු ආකාරයකට කියන්න පුළුවන් විදියක් තමා පිනෝකියෝ විරුද්ධාභාසය.
පිනෝකියො ඔහේ ඉන්න වෙලාවක මෙහෙම කියනවා. ‘ මගේ නහය දික් වෙනවා … ‘
ඔබ පිනෝකියෝ කතාව කියවල තියෙනව නම් දන්නවා පිනෝකියෝ බොරුවක් කියද්දි එයාගේ නහය දික් වෙන බව.
ඒත් දැන් ප්රශ්නය වෙන්නේ පිනෝකියෝ ‘මගේ නහය දික් වෙනවා’ කියන්නේ එසේ නොවන අවස්ථාවකදි. නහය දික් නොවන වෙලාවක මගේ නහය දික් වෙනවා කියන එක බොරුවක්. ඒ කියන්නේ එයා කරන ප්රකාශය, ඒ කියන්නේ ‘මගේ නහය දික් වෙනවා’ කියන ප්රකාශය බොරුවක්.
බොරුවක් කියද්දි පිනෝකියෝගේ නහය දික් වෙන්න ඕන නේ. ඒ නිසා දැන් ඒ කියන්නේ ‘මගේ නහය දික් වෙනවා’ කියන බොරුව කියපු පිනෝකියෝගේ නහය දික් වෙන්න ඕනේ.
හැබැයි දැන් ප්රශ්නේ වෙන්නේ පිනෝකියෝගේ නහය දික් වෙනව නම් එයා ‘මගේ නහය දික් වෙනවා’ කියපු ප්රකාශය බොරුවක් නෙවෙයි. ඒක ඇත්ත. එහෙනම් එයාගෙ නහය දික් වෙන්න බෑ. මොකද එයා බොරුවක් කියල නෑ.
එයා බොරුවක් කියල නැත්නම් එයාගේ නහය දික්වෙන්න බෑ. හැබැයි එහෙම වුණොත් එයා කරන ප්රකාශය ඒ කියන්නේ ‘මගේ නහය දික්වෙනවා’ කියන ප්රකාශය ඇත්ත වෙන්න බෑ. ඇත්ත වෙන්න බැරිනම් ඒ කියන්නේ එයා කියන්නේ බොරුවක් නම් එයාගේ නහය දික් වෙන්න ඕනේ.
මේ සංකීර්ණ ඒත් ඇත්තට ම සරල අවස්ථාව හරියට වටහාගන්න අමාරුයි නම් ටිකක් හිතන්න. ඔබට වටහාගන්න පුළුවන් වෙයි ප්රකාශයක් විසින් එම ප්රකාශය ම විනාශ කරන ආකාරය ගැන.
ශීනෝගේ චලනය පිළිබඳ විරුද්ධාභාසය
ක්රිස්තු පූර්ව 490-430 අතර ජීවත් වූවා යැයි සැලකෙන් ශීනෝගේ මූලික අරමුණ වුනේ ලෝකය බහුත්වයකින් යුතු එකක් නොවේ යන්න පෙන්වා දෙන්න. එහිදී වෙනස් වීම කියන සංකල්පය ඉතා වැදගත්. දේවල් වෙනස් වෙනවා නම් ඒ කියන්නේ ලෝකය විවිධ රූපයන්ට පරිණාමය වෙනවා නම් ලෝකය බහුත්වයකින් යුතුයි. හැබැයි ශීනෝ මේ බව පිළිගත්තේ නෑ. ඔහුට ඕනෑ වුණා විශ්වය බහුත්වයකින් යුතු එකක් නම් එය විරුද්ධාභාසයන් ජනනය කරන්න ඕනේ යන්න ඔප්පු කරන්න. ඉතින් ඒ අරමුණින් ඔහු විරුද්ධාභාස කිහිපයක් ඉදිරිපත් කලා. අවාසනාවකට ඔහුගේ මුල්ම රචනා අපට සොයාගන්න නෑ. ඔහුගේ අදහස් පිළිබඳ ඇරිස්ටෝටල් ආදී දාර්ශනිකයින් ඉදිරිපත් කල මතවාද පමණක් අද ඉතිරිව තිබෙනවා. ඒ අතරිනුත් ඔහු ඉදිරිපත් කල චලනය මායාවක් යැයි පෙන්වාදීමේ තර්ක කිහිපය ඉතා වැදගත්කමකින් යුතු යි. චලනය යන්න ලෝකයේ බහුත්වය පෙන්වන වෙනස්වීමක් සනිටුහන් කරන මූලික යාන්ත්රණයක්. ඒ නිසා ඔහු පෙන්වා දුන්නා චලනය සැබෑවක් බව ගැනීම ම විරුද්ධාභාසයකට මුළ පුරන බව.
ඒ මෙහෙමයි-

ද්විත්ව විරුද්ධාභාසය (en.wikipedia.org)
හිතන්න වස්තුවක් A ලක්ෂයක ඉඳල B ලක්ෂයකට චලනය වෙනව කියල. අපේ සැබෑ අත්දැකීම එම චලනය සැබෑ යාන්ත්රණයක් කියන එක, සිදු විය හැක්කක් කියන එක. මට මම ලියන මේසය ළඟ ඉඳල දොර ළඟට යන්න පුළුවන්. ඒත් ශීනෝ මෙහෙම තර්ක කරනවා.
වස්තුවක් A ලක්ෂයේ ඉඳල B ලක්ෂයට චලනය වෙනවා නම් මුලින් ම වස්තුව A සහ B දුරෙන් අඩක් ගමන් කල යුතු යි. ඒ කතාවත් ඇත්ත. මම මේසේ ළඟ ඉඳල දොර ළඟට යන්න නම් මුලින් ම ඒ අතර දුරින් අඩක් පසු කල යුතුමයි.
අපි හිතමු මේ ගමන තුළ දී වස්තුව A සහ B අතර දුරින් අඩක් ගත කලා කියල. ගමන තවමත් අවසන් නෑ. වස්තුව තවත් දුර ගමන් කල යුතුයි. හැබැයි නැවතත් වස්තුව ඉතිරි දුරින් අඩක් ගමන් කළ යුතු ම යි. ඒ දුරත් ගමන් කලා කියල හිතමු. හැබැයි තවත් දුරක් ඉතිරියි. ඉතින් වස්තුව ඉතිරි දුරින් අඩක් ගමන් කල යුතු යි. ප්රශ්නය, වස්තුව A ලක්ෂයේ සිට B ලක්ෂයට ගමන් කරනවා නම් මෙවන් ‘අඩවල්’ කීයක් ගත කල යුතු ද යන්න. චලනයේ දී වස්තුවක් සෑම විටම ඉතිරිවන දුරෙන් අඩක් ගෙවිය යුතු යි. ඒ කියන්නේ වස්තුව කොපමණ B ලක්ෂයට ළඟා වෙමින් සිටියත් ඉතිරි දුරවල් අවසාන නොවන බව. ඒ කියන්නේ වස්තුවක් A ලක්ෂයේ සිට B ලක්ෂයට ගමන් කිරීමට අනන්ත වතාවක් උත්සහ කල යුතු බව. ප්රශ්නය පරිමිත කාලයක දී අපරිමිත වාර ගණනක කාර්යයක් කොට නිමා කල හැකි ද යන්න. ශීනෝගේ පිළිතුර වූයේ නැත යන්නයි.
ඒ කියන්නේ වස්තූන් චලනය වෙන ලෙස ගැනීම විරුද්ධාභාසයක් බව ඔහු ඔප්පු කරනවා. ඔහුට අනුව චලනය යන අත්විඳීම මායාවක් පමණයි, එය සැබෑවක් නෙවෙයි. එය සැබෑවක් ලෙස ගැනීම විරුද්ධාභාසයකට තුඩු දෙනවා.
ශීනෝගේ දෙවැනි විරුද්ධාභාසී තර්කය තමා ‘ඇකිලීස් සහ ඉදිබුවා’ නමින් හඳුන්වන තර්කය
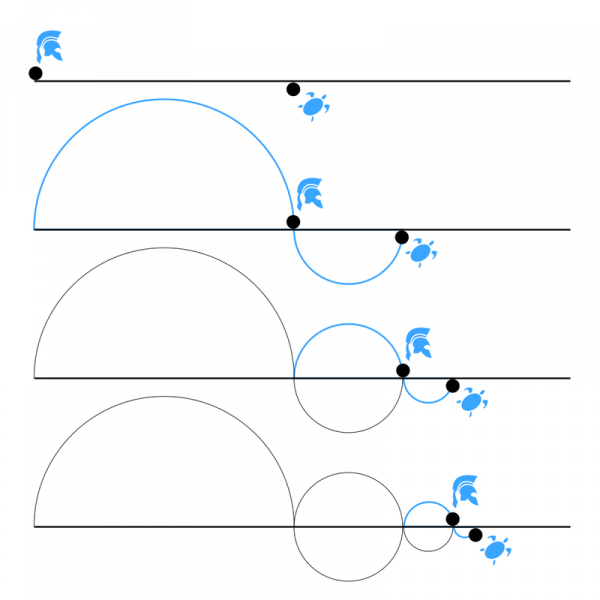
ඇකිලිස් සහ ඉදිබුවා පිළිබඳ විරුද්ධාභාසය (en.wikipedia.org)
ඇකිලීස් කියන්නේ ග්රීක රණශූරයෙක්. ඔහුට වේගයෙන් දුවන්න පුළුවන්. මේ බව දැන දැනත් ඉදිබුවෙක් ඒ කියන්නේ ගොඩ වසන ඉබ්බෙක් ඔහුට අභියෝග කරනවා රේස් එකක් දුවන්න. ඇකිලීස් බොහොම අවඥාවෙන් රේස් එකට කැමති වෙනවා. මොකද ඔහුගේ ජයග්රහණය සක් සුදක් සේ පැහැදිලියි.
හෙමින් ගමන් යන ඉදිබුවා ඇකිලීස්ට මෙහෙම කියනවා. ‘මං හෙමින් යන එකා. ඉතින් මට රේස් එක ආරම්භයේ දී පොඩි චාන්ස් එකක් දෙන්න. මම ඔබට වඩා මීටරයක් ඉදිරියෙන් තරඟය ආරම්භ කරන්න ද ?’
ඇකිලීස්ට ඉදිබුවා පහුකරන්න යන්නේ එක පියවරක් පමණයි. ඉතින් ඇකිලීස් ආයෙත් බොහොම අවඥාවෙන් එකඟ වෙනවා.
ඒ අනුව තරඟය ආරම්භ වෙනවා. ඉදිබුවා ඇකිලීස්ට වඩා මීටරයක් ඉදිරියෙන්. දෙදෙනාම එක වෙලාවෙ තරඟය ආරම්භ කරනවා. ශීනෝ කියන විදියට අපිට කොයි තරම් විශ්වාස වුණත් ඇකිලීස් කොයි තරම් වේගෙන් දිව්වත් ඔහුට ඉදිබුවා ව පහුකරන්න බෑ. ඒ ඇයි ?
දෙදෙනා ම එක ම වේලාවේ තරඟය ආරම්භ කරනවා. වේගවත් ඇකිලීස් කෙටිකාලයක දි ඉදිබුවා හිටපු තැනට ඒ කියන්නෙ මීටරයක දුර ඉදිරියට යනවා. හැබැයි තවමත් ඉදිබුවා ඉස්සරහින්. මොකද ඇකිලිස් මීටරයක් දුර යන්න ගත වුණු කාලයෙ දි ඉතා ම කුඩා දුරක් වුණත් ඉදිබුවා ඒක ගිහින් තියෙනවා.
දැන් ඉදිබුවා ඉතා ම කුඩා දුරක් ඉදිරියෙන්, ඇකිලිස් පිටුපසින්. වේගවත් ඇකිලීස් මේ ඉතා කෙටි දුර ඉතා කෙටි කාලයකින් තරණය කරනවා. හැබැයි මතක තියාගන්න ඒ ඉතා කෙටි කාලෙ දි ඉදිබුවත් ඊටත් වඩා කෙටි දුරක් ඉදිරියට චලනය වී ඇති බව. ඇකිලීස් ඒ කෙටි දුරත් ඉදිරියට යනවා ඒත් ඒ කාලය ඇතුලත ඉදිබුවා තවත් ඉස්සරහට යනවා.
ඔබට පැහැදිලි ද, ඉදිබුවා සහ ඇකිලීස් අතර දුර ක්රමයෙන් අඩු වුණත් සෑම විට ම ඉදිබුවා ඉදිරියෙන් බව. තර්කය කෙසේ වුවත් සැබෑ ලෝකයේ දි ඇත්තට ම ඇකිලීස්ට ඉදිබුවා පසුකරගෙන යන්න පුළුවන් ඉතා ම පහසුවෙන්. මේක විරුද්ධාභාසයක් වෙන්නේ ඒ නිසා.
මේ සරල විදියට පෙනෙන ප්රශ්නය වැඩකට නැති දෙයක් ලෙස සලකා දමන්න බෑ. මොකද අවුරුදු දෙදහක් තුන්දහක් ගත වුණත් තවමත් මේ සම්බන්ධයෙන් ශාස්ත්රීය පර්යේෂණ පත්රිකා එළි දැක්වෙනවා.
මේ උත්සහයන් සියල්ල සලකා බලා පර්යේෂණ පත්රිකාවක් ඉදිරිපත් කරන කෙවින් බ්රවුන් 2010 දී මෙහෙම ලියනවා.
“ඉතිහාසය පුරා ම ශීනෝගේ විරුද්ධාභාසයන්ට පිළිතුරු සැපයී තියෙනවා, අවසන් විසඳුම් ඉදිරිපත් කර තිබෙනවා. නමුත් අප ඒවා විසඳා ඇතැයි සිතීම වැරදියි. මෙම චලනය පිළිබඳ විරුද්ධාභාස ඒවායේ සරලකම මෙන් ම විශ්වීයකම නිසා ම අපේ දාර්ශනික මතවාද පිළිබිඹු වන රොෂැක් රූප සේ කටයුතු කරනවා.”

රොෂැක් රූප: තීන්ත බිඳුවේ සමමිතික රටාවට නිසඟ තේරුමක් සහ හැඩයක් නැත. එයට තේරුම ලබා දෙන්නේ අප ය. (gamedev.stackexchange.com)
තාර්කික ගැටළු ගැන අපි කතා කල යුත්තේ සහ පිළිතුරු සෙවිය යුත්තේ ජනප්රිය වහරෙන් කියන විදියට ‘ඔළුව කුරුවල් කර ගැනීම’ සඳහා නොවේ. අපි හිතන්නේ ද කතා කරන්නේ ද භාෂාව භාවිතයෙන්. පරිඝණක භාෂාවක සිට සංඥා භාෂාවක් දක්වා ඕනෑම සන්නිවේදන ක්රමයක් තර්කාණුකූල විය යුතුයි. මොකද තාර්කික බවක් නැති පූර්ණ බවක් නැති ප්රකාශයක් හුදු නන්දෙඩවිල්ලක් පමණක් වන නිසා ඉන් කිසිම අදහසක් සන්නිවේදනය නොවන බැවින්. අපි තර්කශාස්ත්රයේ සහ දර්ශනයේ ඇති මේ පටලැවීම් කතාකරන්නේ මෙම අදහස හිතේ තබාගෙන, කොයි තරම් වියුක්ත දේවල් ලෙස පෙනුනත් ප්රායෝගික ලෝකය හැඩ ගැහී ඇත්තෙම මේ වගේ සංකල්ප පිළිබඳ අපගේ වටහාගැනීමත් එක්ක.
අපි තවත් විරුද්ධාභාස කිහිපයක් ගැන කතා කරමු, වෙනත් ලිපියකින්.








