
e = 2.718218…
এই e এর সাথে মাধ্যমিক গণিত হতে আমরা সকলেই পরিচিত। ln e = 1 কিংবা dy/dx(e^x) = e^x ইত্যাদি। e নিয়ে বিচিত্র সব সূত্র আমাদের অনেককেই ভাবিয়েছে এর মাহাত্ম্য নিয়ে। এই e হচ্ছে অয়লার’স নাম্বার। গণিতবিদ লিওনার্দ অয়লার (Leonhard Euler) যার প্রবক্তা।
পাই এর জন্য π, √-1 এর জন্য i , যোগের জন্য Σ (সিগমা) সহ গণিতে নানা প্রতীকের সূচনা করেন অষ্টাদশ শতাব্দীর এই গণিতবিদ। তিনি তত্ত্বীয় গণিতের অন্যতম প্রবর্তক। তিনি প্রায় ৫০০ টির উপরে গবেষণা প্রকাশ করেন। অয়লার সংখ্যাতত্ত্ব, ইন্টিগ্রাল ক্যাল্কুলাস, বলবিদ্যা, আলোকবিদ্যা, জ্যোতির্বিজ্ঞান , প্রবাহী গতিবিদ্যা নিয়েও কাজ করেছেন। তার কাজের মধ্যে অন্যতম হলো কনিগসবার্গের সেতু সমস্যা। এটি সমাধান ও গ্রাফ থিওরি আবিষ্কারের পেছনে এক কৌতূহলোদ্দীপক কাহিনী আছে।

অয়লারের জন্ম ১৭০৭ সালে সুইজারল্যান্ডের বেসেল শহরে। ছাত্রজীবনে তিনি সান্নিধ্য পেয়েছিলেন আরেক বিখ্যাত গণিতবিদ জোহান বারনৌলির (Johann Bernoulli)। কর্মজীবনে অয়লার সেন্ট পিটার্সবার্গ বিজ্ঞান একাডেমি ও বার্লিন একাডেমিতে দায়িত্ব পালন করেন। সেন্ট পিটার্সবার্গে থাকাকালে জার্মানির কনিগসবার্গ (Königsberg ) শহর থেকে তিনি এক চিঠি পান কনিগসবার্গ ব্রিজ সংক্রান্ত এক সমস্যা নিয়ে। কনিগসবার্গ শহরটি প্রেগেল (Pregel) নদী দিয়ে বেষ্টিত। নদীটি শহরটিকে চার ভাগে ভাগ করে, যেখানে রয়েছে মূল দুটি ভুখণ্ড ও দুটি দ্বীপ। সবগুলো অংশ ৭ টি আলাদা ব্রিজ দ্বারা সংযুক্ত ছিল। শহরবাসীদের অবসর মনে এই প্রশ্ন আসে যে, কেও কোন রুট অনুসরণ করলে যে কোনো একটি জায়গা থেকে যাত্রা শুরু করে, কোনো ব্রিজে একাধিক বার না গিয়ে, ৭টি ব্রিজই পাড়ি দিতে পারবে? সমস্যাটি চিত্রের সাহায্যে ব্যাখ্যা করা যায়-
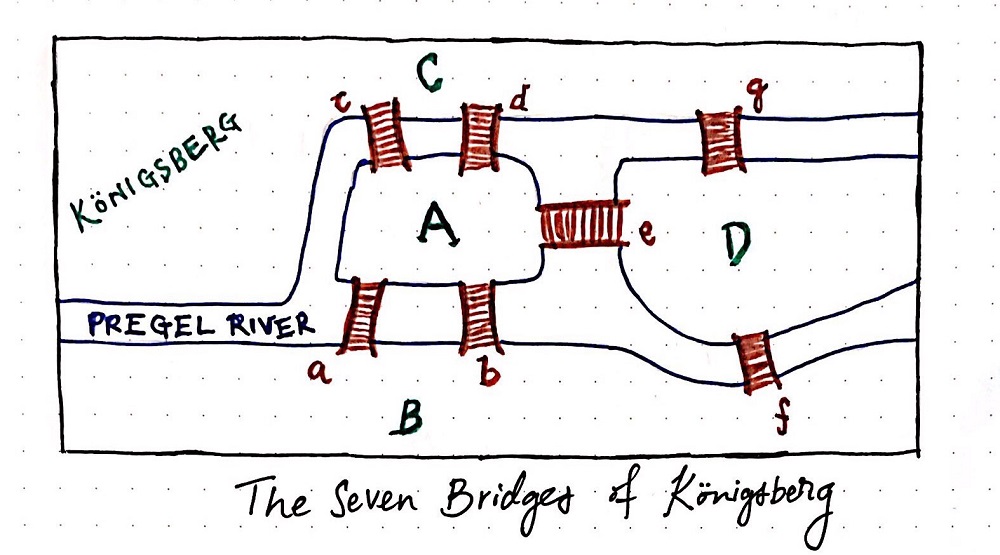
মূল ভূখণ্ড A, B, C ও D চারটি ভাগে বিভক্ত। ভাগগুলো ৭টি ব্রিজ দ্বারা সংযুক্ত। A, B, C ও D যেকোনো স্থান থেকে শুরু করে, সাতটি ব্রিজই কেবলমাত্র একবার পাড়ি দিয়ে যাত্রা শেষ করা কি সম্ভব (অবশ্যই সাঁতার না কেটে)? পাঠক, চিত্রটি দেখে চেষ্টা করে দেখুন, প্রায় ৩০০ বছর আগের এই ধাঁধা সমাধান করতে পারেন কিনা।
ঘাম ছুটে যাওয়ারই কথা। আপাত দৃষ্টিতে এই ধাঁধাটি সমাধান করা সম্ভব মনে হলেও আসলে এর কোনো সমাধান নেই। প্রতিটি ব্রিজের উপর দিয়ে কেবলমাত্র একবার যাত্রা করে ৭টি ব্রিজ পাড়ি দেওয়া সম্ভবই না। অয়লার প্রথমে সমস্যাটিকে তেমন গুরুত্ব দেননি। তিনি বলেন, গণিতের সাথে এর কোনো সম্পর্কই নেই। পরে তিনি এই সাধারণ সমস্যাটির সমাধান দেন এবং এটি থেকেই অয়লার প্রবর্তন করেন গণিতের জিওমেট্রি অব পসিশন, যা পরে গ্রাফ থিওরি নামে পরিচিতি লাভ করে। ডেটা চার্ট, বার বা লাইন গ্রাফ বলতে যেটি বুঝায়, এই থিওরি সেটি ব্যাখ্যা করে না আসলে। গ্রাফ থিওরি অনেক বিন্দু বা পয়েন্টস (points) এর নেটওয়ার্ক নিয়ে কাজ করে।
এটি ব্যাখ্যা করার জন্য অয়লার প্রতিটি ভূমিকে (মূল ভূখণ্ড ও দ্বীপ) এক একটি বিন্দু বা নোড (node) বা vertex হিসেবে বিবেচনা করেন। যেকোনো দুটি নোডের কানেক্টিং রেখা তথা ব্রিজগুলো হচ্ছে লাইন বা এজেস (edges)। অয়লার সমস্যাটি এভাবে উপস্থাপন করেন-
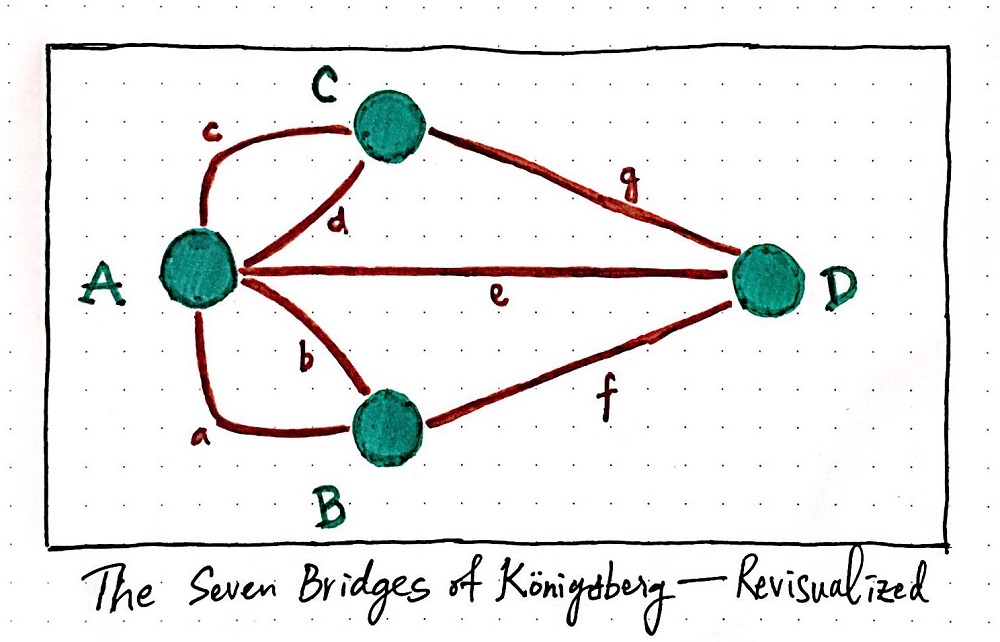
অয়লার দেখান যে, প্রথম ও শেষ নোড ছাড়া বাকিগুলো জোড় সংখ্যক এজ-এর সাথে যুক্ত থাকলে সবকটি এজ এক বার মাত্র পাড়ি দিয়ে যাত্রা সম্ভব। এ রকম রুটকে বলে অয়লারিয়াল পাথ (Eulerian path)। চলার পথে একটি ব্রিজ দিয়ে একটি ভূখণ্ডে ঢোকা হচ্ছে, এবং আরেকটি দিয়ে বের হওয়া যাচ্ছে। এভাবে যদি একটি ভূখণ্ডের সাথে ব্রিজগুলো জোড়ায় জোড়ায় থাকে (in pairs), তাহলে প্রতিটি ব্রিজ একবার ব্যবহার করেই একটি ভূখণ্ডে প্রবেশ ও বাহির সম্ভব। একটি নোড (ভূখণ্ড) যে কয়টি এজের (ব্রিজের) সাথে যুক্ত তাকে নোডের ডিগ্রি বলে অভিহিত করা যায়। অয়লার বলেন, এ রকম প্রতিটি এজ একবারমাত্র পাড়ি দিয়ে যাত্রা তথা অয়লারিয়ান পথ সম্ভব, যদি এই ২টি স্বীকার্যের যেকোনো একটি সত্য হয়-
- কেবল ২টি বিজোড় ডিগ্রি সম্বলিত (শুরুর ও শেষের) নোড, বাকিগুলোর ডিগ্রি হতে হবে জোড়।
- সবগুলো নোডের ডিগ্রি জোড় হয় (তখন শুরুর ও শেষ বিন্দু একই হবে, এ রকম লুপকে বলে অয়লারিয়ান সার্কিট)।
কনিগসবার্গে এই শর্তগুলো পূরণ হয়নি বলে এর সমাধানও সম্ভব নয়। A, B, C ও D চারটি ভূখণ্ডের প্রতিটির সাথেই বিজোড় সংখ্যক ব্রিজ যুক্ত (5, 3, 3 ও 3)। কিন্তু যদি আর একটি ব্রিজ সহ মোট ৮টি ব্রিজ থাকতো, তাহলেই প্রতিটি ব্রিজ একবার করে পাড়ি দিয়ে শুরুর বিন্দুতে আসা সম্ভব হতো, বা একটি অয়লারিয়ান পাথ তৈরি হতো।
গ্রাফ থিওরি পরবর্তীতে বিভিন্ন ক্ষেত্রে কাজে এসেছে। এটি মূলত বিভিন্ন ডেটা বা বস্তুর মধ্যে সম্পর্ক নিয়ে আলোচনা করে। বিভিন্ন বিন্যাস, নেটওয়ার্ক, অপ্টিমাইজেশন, ম্যাচিং ও অপেরাশনাল প্রব্লেমের সমাধানে এই থিওরি কাজে আসে। গুগল ম্যাপে দুটি জায়গার মাঝের শর্টেস্ট পাথ বের করেতে কাজে লাগে এই থিওরি। কম্পিউটার বিজ্ঞানে নানা এলগোরিদম বিশ্লেষণে গ্রাফ থিওরি একটি গুরুত্বপূর্ণ হাতিয়ার।
একটি নেটওয়ার্কে সংক্ষিপ্ততম পথ খোঁজার জন্যও গ্রাফ থিওরি ব্যবহৃত হয়। তড়িৎ প্রকৌশলে সার্কিট ডিজাইন ও সমাধানে গ্রাফ থিওরির ব্যবহার অনস্বীকার্য। এছাড়াও পরিসংখ্যানের বিবিধ সমস্যা সমাধানে, জটিল সিমুলেশনের ত্রিমাত্রিক ছবি ব্যাখ্যায়, আণবিক গঠন বিশ্লেষণে, মিনিমাইজেশন প্রবলেম সমাধানে ইত্যাদি বিভিন্ন জায়গায় গ্রাফ থিওরির প্রয়োগ রয়েছে।

যে কনিগসবার্গের কল্যাণে গণিতের এক নতুন ধারার সূচনা হয়, সেই শহরটি আজ মানচিত্রে নেই। দ্বিতীয় মহাযুদ্ধের সময় মিত্রবাহিনীর বোমা বর্ষণে শহরটি মারাত্মকভাবে ক্ষতিগ্রস্ত হয়। যুদ্ধের পরে এলাকাটি রাশিয়ার দখলে আসে এবং এর নামকরণ হয় কালিনিনগ্রাড। গ্রাফ থিওরির ইতিহাসের সাথে শহরটির পুরোনো নামও ইতিহাসের পাতায় ঠাঁই করে নিয়েছে।
অয়লার তার সারাজীবন কাটিয়ে গেছেন বিভিন্ন গবেষণায়। জীবন সায়াহ্নে অন্ধ অবস্থায়ও অন্যদের সাহায্যে তিনি অনেক গবেষণা প্রকাশ করেন। প্রথিতযশা এই বিজ্ঞানী ১৭৮৩ সালে রাশিয়ায় শেষ নিঃশ্বাস ত্যাগ করেন। তার সম্মানার্থে ইনস্টিটিউট অব কম্বিনেটরিক্স এন্ড ইটস এপ্লিকেশন্স (ICA) গবেষণায় ‘অয়লার মেডেল’ প্রদান করে থাকে। ১৯৭৩ সালে আবিষ্কৃত এক গ্রহাণুর নামকরণ করা হয় ‘২০০২ অয়লার’ নামে।

চিরাচরিত কোনো ঘটনার প্রবাহে, মাঝে মাঝে আকস্মিকই আবিষ্কৃত হয় নতুন কোনো তত্ত্ব, উদয় হয় নতুন এক দিগন্তের। কনিগসবার্গ শহরবাসীর অবসরে কোনো এক কফিহাউসে আলোচিত সাতটি ব্রিজ কেবল একবার পাড়ি দেওয়ার ধাঁধা থেকে গ্রাফ থিওরির মতো গণিতের এক তত্ত্বীয় ধারার সূচনা হয়, যা আজও মানব সভ্যতায় বিভিন্ন সমস্যা সমাধানে ব্যবহৃত হচ্ছে।







