
নৈসর্গিক এই পৃথিবীতে মোহিত হওয়ার মতো অসংখ্য সৌন্দর্যের উৎস ছড়িয়ে ছিটিয়ে রয়েছে। কখনো হয়তো আমরা মুগ্ধ হই প্রকৃতির অবারিত রুপ এবং সুষমায়। প্রকৃতির সেই রুপ খুঁজে পাওয়া যায় অসীম নীল আকাশে। নীল আকাশের পটভূমিতে ভেসে বেড়ানো পেঁজা তুলার মতো সাদা মেঘে, জালের মতো ছড়িয়ে থাকা নদী-নালায়, সৈকতে আছড়ে পড়া ঢেউয়ে বা সবুজ বৃক্ষরাজিতে। আবার কখনো হয়ত মুগ্ধ হই মানবসৃষ্ট নান্দনিক কোনো শিল্পকর্মে। কখনো বা কম্পিউটারের পর্দায় দেখা দেদীপ্যমান জটিল কিন্তু দারুণ সুন্দর আর রঙিন কোনো নকশায়। আপনি আপনার কম্পিউটারের স্ক্রিনকে সুশোভিত করতে প্রাকৃতিক দৃশ্য ছাড়াও শৈল্পিক কোনো নকশাও নিশ্চয়ই ব্যবহার করেছেন। প্রাকৃতিক সৌন্দর্যমন্ডিত কোনো দৃশ্যের দিকে আমরা যেমন মুগ্ধবিস্ময়ে তাকিয়ে থাকি তেমনি কম্পিউটার প্রোগামকে কাজে লাগিয়ে নির্মিত অসম্ভব উজ্জ্বল আর রঙিন এই নকশাগুলোও এতটাই সুন্দর হয় যে, এগুলোর দিকে মন্ত্রমুগ্ধ হয়ে তাকিয়ে থাকতে বাধ্য হতে হয়। অনেকেই হয়তো জানেন আপনার পরিচিত এই রঙ-বেরঙের জটিল কারুকাজকে ফ্র্যাক্টাল বলে।

একটি ফ্র্যাক্টাল চিত্র; Source:flashlarevista.com
ব্যস! ফ্র্যাক্টালের পরিচয় কি শুধু এটাই যে এরা প্যাঁচবহুল বিচিত্র কিছু নকশা? একদমই নয়। ফ্র্যাক্টালের সাথে ঘনিষ্ঠ সংযোগ আছে গণিত, জ্যামিতি এবং প্রকৃতির অজানা অনেক রহস্যের। ফ্র্যাক্টালের বহুল ব্যবহার আছে বিজ্ঞান ও প্রযুক্তির নানা ক্ষেত্রে। ফ্র্যাক্টাল দিয়ে তৈরী করা সম্ভব অনিন্দ্যসুন্দর আস্ত একটি জগত।
ফ্র্যাক্টাল আসলে কী?
পাঠক, স্বাগতম ফ্র্যাক্টালের দুনিয়ায়। ফ্র্যাক্টাল হচ্ছে চমকপ্রদ ও অদ্ভুতুড়ে কিছু জ্যামিতিক আকৃতি। এটি এমন একধরনের জ্যামিতিক গঠন যা ভিন্ন ভিন্ন স্কেলের সাপেক্ষে পরিবর্তিত হয় না, একইরকম থাকে। একে সংকুচিত বা বর্ধিত যাই করা হোক না কেন শেষপর্যন্ত একই গঠন পাওয়া যায়। এর প্রতিটি ক্ষুদ্র অংশ মূল ও বৃহৎ গঠনটির মতোই হয়। ফ্র্যাক্টাল একটি অসীম গোলকধাঁধা কিন্তু অতি সাধারণ একটি নকশা থেকে তৈরী হয়। সাধারণ সেই নকশা বারবার আঁকতে থাকলে জটিল একটি নকশার রুপ পায়। এই জটিল নকশার পুনরাবৃত্তি করতে থাকলে একসময় সেই নকশা হয়ে যায় অসীম আকৃতির। অসীম সেই নকশার প্রতিটি অংশ আবার একই হয়। এই বিচিত্র নকশাই হচ্ছে ফ্র্যাক্টাল।
ভালোভাবে বুঝতে পারলেন না, তাই না? আচ্ছা, একটি উদাহরণের প্রসঙ্গ আনা যাক। ফার্ন দেখেছেন নিশ্চয়ই?

ফার্ন; Source: biology questions and answers
উপরের ফার্নের ছবিটি আবার দেখুন। ভালোভাবে খেয়াল করুন। ফার্নের গঠনপ্রকৃতি কিন্তু বেশ জটিল। কিন্তু ফার্নের প্রতিটি পত্রক ফার্নের একটি শাখার মতোই দেখতে। প্রতিটি শাখা আবার পুরো ফার্নটির মতো দেখতে। আসলে ফার্ন একটিই মৌলিক আকৃতির পুনরাবৃত্তির মাধ্যমে গঠিত হয়। ফার্নের এই বৈশিষ্ট্যটি ফ্র্যাক্টালেরও বৈশিষ্ট্য। একে বলা হয় স্বঅনুরুপতা (self-similarity)। তাহলে বলা যায়, ফার্ন একটি ফ্র্যাক্টাল।

বেনোইট মেনডেলব্রট; Source:wikimedia commons
‘ফ্র্যাক্টাল’ শব্দটি প্রথম ব্যবহার করেন গণিতবিদ বেনোইট মেনডেলব্রট, ১৯৭৫ সালে। ল্যাটিন ‘Fractus‘ শব্দের অর্থ ভাঙা বা চিড় ধরা। প্রাকৃতিক অনেক অনিয়মিত আকৃতিকে ইউক্লিডীয় জ্যামিতি ব্যাখা করতে পারে না। সেইসব আকৃতিকে গাণিতিকভাবে ব্যাখা করতে প্রবর্তিত হয় গণিতের নতুন শাখা ‘Fractal Geometry‘। গণিতের অন্যান্য শাখায় যেখানে জটিল, বিরক্তিকর সমীকরণ বা সূত্রের ছড়াছড়ি লক্ষ্য করা যায়, ফ্র্যাক্টাল জ্যামিতি সেখানে একেবারেই অন্যরকম। এখানে গণিত এবং শিল্পের এক অভাবনীয় সমন্বয় ঘটেছে।
ফ্র্যাক্টালের অন্যতম গুরুত্বপূর্ণ বৈশিষ্ট্য হচ্ছে স্ব-অনুরুপতা। এছাড়াও কিছু সাধারণ বৈশিষ্ট্য রয়েছে যেগুলো থাকলে কোনো আকৃতি বা গঠনকে আমরা ফ্র্যাক্টাল বলবো। এই বৈশিষ্ট্যগুলো চলুন জেনে আসি।
১. অসীম জটিলতা (Infinite intricacy)
১৮৬১ সালে প্রথম ফ্র্যাক্টালের আবিষ্কারের পর পৃথিবীর গণিতজ্ঞ সমাজ দারুণ এক ধাক্কা খেয়েছিলেন। আপনি যদি পেন্সিল দিয়ে একটি আঁকাবাঁকা রেখা আঁকেন দেখতে পাবেন বেশ কয়েকটি কোণ তৈরী হয়েছে যারা বেশ কিছু সরলরেখা দিয়ে পরস্পরের সাথে যুক্ত আছে। জার্মান গণিতবিদ কার্ল ওয়্যারস্ট্রাস এমনই একটি বক্ররেখা এঁকেছিলেন। সেটি অনেক বেশি বক্র ছিল। কিন্তু তা আসলে তৈরী হয়েছিল ছোট ছোট কিছু কোণ দিয়েই।
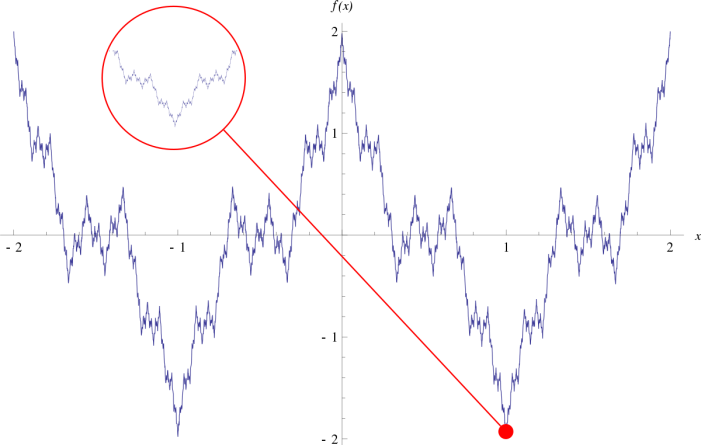
কার্ল ওয়ারস্ট্রাসের আঁকা প্রথম ফ্র্যাক্টাল; Source: wikimedia commons
একটি বক্ররেখাকে যত বেশি বর্ধিত করবেন এটি তত বেশি বক্র আর জটিল হতে থাকবে। একসময় এর জটিলতা অসীম আকার ধারণ করবে। তবে তা অসীম কোণের স্রোতধারা ছাড়া আর কিছুই নয়। গণিতবিদেরা ওয়্যারস্ট্রাসের এই আকৃতিকে ‘অস্বাভাবিক ও বিকারগ্রস্থ’ আখ্যা দেন কারণ এটি ক্যালকুলাসের প্রতিষ্ঠিত নিয়ামকানুনকে প্রকাশ্যে অমান্য করার ধৃষ্টতা দেখিয়েছিল! জটিল হিসাবনিকাশ করার ক্ষমতাসম্পন্ন আধুনিক কম্পিউটার আবিষ্কারের আগপর্যন্ত এটি একটি দুর্বোধ্য আকৃতিই ছিল যা আঁকা ছিল ভীষণ কষ্টকর। কম্পিউটারের বদৌলতেই ফ্র্যাক্টাল সাম্রাজ্যের আজকের অগ্রগতি সম্ভব হয়েছে।
২. বিবর্ধিত প্রতিসাম্য (Zoom Symmetry)
“আমার মনে হয়েছে এমন সব বস্তু দিয়ে এমন এক জ্যামিতি তৈরী করছি যাদের কোনো জ্যামিতিই নেই” -বেনোইট মেনডেলব্রট
ফ্র্যাক্টাল জ্যামিতিকে গণিতের নতুন একটি শাখা হিসেবে প্রতিষ্ঠা করতে সবচেয়ে বেশি অবদান যার তিনি হলেন পোলিশ বংশোদ্ভুত বিজ্ঞানী বেনোইট মেনডেলব্রট। তিনি ১৯৬০ এর দশকে IBM এ কাজ করতেন। সেই সুবাদে এই কোম্পানীর শক্তিশালী কম্পিউটারগুলোকে কাজ লাগিয়ে ফ্র্যাক্টালের নতুন ও অদ্ভুত জগতে অবাধে বিচরণ করতে পারতেন। এ পর্যন্ত আবিষ্কৃত পৃথিবীর সবচেয়ে জটিল ফ্র্যাক্টাল হচ্ছে ‘মেনডেলব্রট সেট’। এটি এতটাই জটিল যে কম্পিউটার ছাড়া আঁকা সম্ভব নয়। কিছু কিছু কম্পিউটার প্রোগ্রাম এই ফ্র্যাক্টাল তৈরী কিছুটা সহজ করেছে। এই প্রোগামগুলো আপনাকে নতুন ধরনের এক প্রতিসাম্যের সাথে পরিচয় করিয়ে দেবে যা সাধারণ কোনো প্রতিসম আকৃতির চেয়ে একেবারেই আলদা। গণিতে প্রতিসাম্য কথাটার মানে হচ্ছে, একটি আকৃতিকে যেভাবেই কাটা হোক না কেন তা একই রকম দেখাবে। ফ্র্যাক্টালের অফুরন্ত ঘোর প্যাঁচজনিত জটিলতা এই বিচিত্র প্রতিসাম্যের জন্য দায়ী। ফ্র্যাক্টালের একটা ক্ষুদ্র অংশকে বর্ধিত করলে একই আকৃতির দেখা মেলে।
৩. সরলতা থেকে অসীম জটিলতা
“ফ্র্যাক্টালের অতল বিস্ময়ের জন্ম হয় কিছু সহজসরল নিয়মকানুনের অসীম সংখ্যক পুনরাবৃত্তি থেকে।”- বেনোইট মেনডেলব্রট।
ফ্র্যাক্টাল খুব জটিল একটি জ্যামিতিক আকৃতি। কিন্তু এর অনিঃশেষ জটিলতার উদ্ভব হয় অতি সাধারণ আকৃতি থেকে। মেনডেলব্রটের মতোই ফ্র্যাক্টাল জ্যামিতির আরেক প্রভাবশালী গবেষক হচ্ছেন মাইকেল বার্নশলে। বার্নশলে তার ১৯৮৮ সালে প্রকাশিত “Fractals Everywhere” গ্রন্থে ‘Chaos Game‘ নামের একটি এলগরিদমের উল্লেখ করেছেন যা কিনা জানা নকশা থেকে দ্রুত জটিল ফ্র্যাক্টাল তৈরী করতে পারে। বার্নশলে ফার্ন এর একটি উৎকৃষ্ট উদাহরণ।

বার্নশলে ফার্ন; Source:the conversation
এতে ৪টি সরল ম্যাপ ব্যবহার করে অসংখ্য ফার্ন তৈরী করা যায়। প্রকৃতিতেও আমরা এই নিয়মের প্রতিফলনই দেখতে পাই।
৪. ভগ্নাংশ মাত্রা (Fractional Dimension)
“প্রকৃতি যেন গণিতবিদদের প্রতি ক্রুর হাসি ছুঁড়ে দিয়েছে। উনবিংশ শতাব্দীর গণিতবিদদের হয়তো কল্পনাশক্তির অভাব ছিল কিন্তু প্রকৃতির কখনো ছিল না” – ফ্রীম্যান জন ডাইসন।
ফ্র্যাক্টালের সবচেয়ে চমকপ্রদ বৈশিষ্ট্য হচ্ছে এটি পূর্ণমাত্রার নয়, এটি হয় ভগ্নাংশ মাত্রার। মানে এটি একমাত্রিক (শুধু দৈর্ঘ্য আছে) বা দ্বিমাত্রিক (দৈর্ঘ্য এবং প্রস্থ আছে) নয়, বরং এর মাঝামাঝি কিছু। মাত্রা (Dimension) কী সে সস্পর্কে আরেকটু স্বচ্ছ ধারণা নেয়া যাক। মাত্রা বলতে গণিতে বোঝানো হয় কোনো বস্তু বা আকৃতি কতটা অমসৃণ বা মসৃণ হবে কিংবা কতটা জায়গা দখল করে থাকবে। যেমন – একটি কাগজ দ্বিমাত্রিক এবং একটি গোলক ত্রিমাত্রিক বস্তু।
এর অর্থ হচ্ছে, একটি কাগজ যতটুকু জায়গা জুড়ে থাকবে একটি গোলক তার চেয়ে বেশি জায়গা জুড়ে থাকবে। এখন কাগজটাকে মুচড়ে ফেলুন। এখন দেখবেন এটি ফ্র্যাক্টলের মতো অনিয়মিত আকৃতি ধারণ করেছে। এটি কাগজের চেয়ে বেশি জায়গা দখল করছে, কিন্তু গোলকের চেয়ে কম। অর্থাৎ এর মাত্রা হচ্ছে ২ বা ৩ নয়, প্রায় ২.৫! প্রকৃতিতে এই রহস্যময় ভাঙা মাত্রার দেখা মেলে। ফার্নের কথাই ধরুন না। এর মাত্রাও কিন্তু ২ ও ৩ এর মাঝামাঝি। আবাার আমাদের প্রধান শ্বসনঅঙ্গ ফুসফুসের মাত্রা ২.৭! ফুসফুসের এই দুর্বোধ্য মাত্রাবিন্যাসই একে অল্প আয়তনে (কয়েকটি টেনিস বলের সমান) বিশাল জায়গা (কয়েকটি টেনিস কোর্টের সমান) জুড়ে থাকতে সহায়তা করেছে। তাই দুটো ফুসফুস বিশাল পরিমাণ বাতাস ধারণ করে আপনাকে বাঁচিয়ে রাখতে পারে।
তাত্ত্বিক আলোচনা আর না বাড়িয়ে চলুন এবার পরিচিত হওয়া যাক বহুল ব্যবহৃত কিছু ফ্র্যাক্টালের সাথে।
১. শেরপিনস্কি ট্রায়াঙ্গল
শেরপিনস্কি ট্রায়াঙ্গল বা গ্যাসকেট একটি ফ্র্যাক্টাল নকশা। ১৯১৬ সালে পোলিশ গণিতবিদ শেরপিনস্কি এটি আবিষ্কার করেন। এক্ষেত্রে প্রথমে একটি বড় কালো ত্রিভুজ নেয়া হয়। ত্রিভুজটির মাঝখান থেকে উল্টানো ত্রিভুজ কেটে নেয়া হয়। এই ত্রিভুজটি হয় সাদা রঙের। এতে বড় ত্রিভুজটি তিনটি অংশে বিভক্ত হয়।

শেরপিনস্কি একটি ত্রিভুজ থেকে অসীম সংখ্যক ত্রিভুজ তৈরী হয়; Source:reddit
প্রতিটি কালো ত্রিভুজ থেকে আবার একটি করে উল্টানো ত্রিভুজ কেটে নেয়া হয়। এই প্রক্রিয়া চলতেই থাকে। এভাবে প্রথমদিকে কালো ত্রিভুজের সংখ্যা গুণতে পারলেও একসময় আর গুণতে পারবেন না। কালো ত্রিভুজ হয়ে যাবে অসীম সংখ্যক। এই ত্রিভুজগুলোকে বর্ধিত করলে (Zoom In) ত্রিভুজের প্রাচুর্য্য দেখে বিস্ময়ে হতবাক হয়ে যেতে হয়।
২. মেনডেলব্রট সেট
মেনডেলব্রট সেট হচ্ছে সবচেয়ে জটিল ফ্র্যাক্টাল। ফ্র্যাক্টাল জ্যামিতি বিকশিত হয়েছে যার হাত ধরে সেই বেনোইট মেনডেলব্রটের অনন্য সাধারণ আবিষ্কার হচ্ছে এই ফ্র্যাক্টালটি।
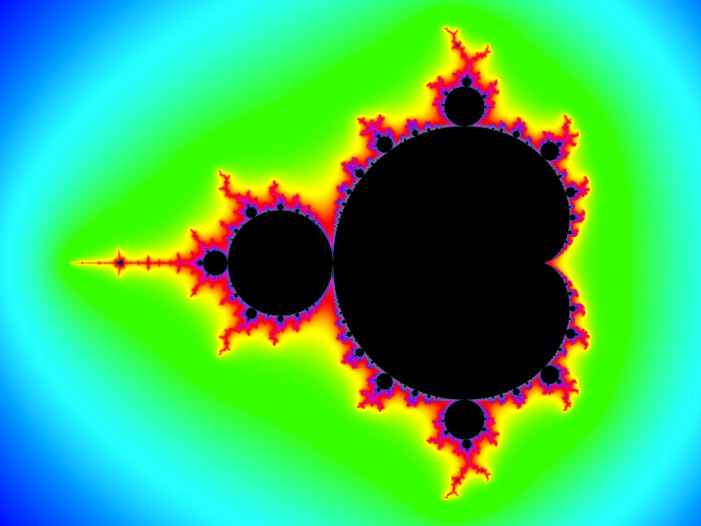
মেনডেলব্রট সেট; Source:wired.com
ভীষণ জটিল এই ফ্র্যাক্টালটি অনেক জটিল গাণিতিক হিসাব থেকে তৈরী হয়। আসলে একটি সাধারণ সূত্রের অসাধারণ গ্রাফিক্যাল প্রদর্শনী হচ্ছে মেনডেলব্রট সেট। সমীকরণটি হচ্ছে,
![]()
এখানে, C ও Z হচ্ছে যৌগিক সংখ্যা এবং n শূন্য কিংবা ধনাত্মক পূর্ণসংখ্যা। এই পর্যায়ে যৌগিক সংখ্যা সম্পর্কে কিছু কথা না বললেই নয়। যৌগিক সংখ্যার দুটি অংশ থাকে। একটি বাস্তব সংখ্যা, আরেকটি অবাস্তব বা কাল্পনিক সংখ্যা (Imaginary Number), যাকে i দিয়ে চিহ্নিত করা হয়। কাল্পনিক সংখ্যা বলতে সেসব সংখ্যাকে বোঝায় যাদের বর্গমূল হয় নেতিবাচক (Negative)। যেমন a+bi একটি যৌগিক সংখ্যা। এখানে bi অংশটি কাল্পনিক সংখ্যা। মেনডেলব্রট সেটে এই যৌগিক সংখ্যাই ব্যবহার করা হয়।
যৌগিক সংখ্যার যেহেতু দুটি অংশ থাকে, তাই মেনডেলব্রট সেটের জন্য যে গ্রাফটি ব্যবহার করা হয় সেটিরও দুটি অংশ থাকে- X অক্ষ এবং Y অক্ষ। মেনডেলব্রটের সমীকরণে C ধ্রুব থাকে। C এর স্থানে একটি নির্দিষ্ট সংখ্যা নেয়া হয় যা স্থির থাকে। কিন্তু Z এর মানের ভিন্নতার কারণে সমীকরণ থেকে প্রাপ্ত মান বিভিন্ন হয়। এই মানগুলোকে গ্রাফে বসানো হয় এবং নির্দিষ্ট একটি রং দিয়ে চিহ্নিত করা হয়। এভাবে হাজার হাজার মান বসিয়ে একটি আকৃতি পাওয়া যায়। এই আকৃতি প্রবর্ধিত করতে থাকলে অসীম, জটিল নকশা পাওয়া যায়।
৩. জুলিয়া সেট
জুলিয়া সেট আবিষ্কার করেন গণিতবিদ গ্যাস্টন জুলিয়া। জুলিয়া সেটেও মেনডেলব্রট সেটের মতো একই সমীকরণ ব্যবহার করা হয়। পার্থক্য হচ্ছে এখানে Z এর মান স্থির রাখা হয়, পরিবর্তিত হয় C এর মান। এভাবে সমীকরণ থেকে পাওয়া মানগুলো গ্রাফে বসিয়ে দারুণ সুন্দর আর অস্বাভাবিক জটিল সব নকশা পাওয়া যায়।

দৃষ্টিনন্দন একটি জুলিয়া সেট; Source:snt.utwante.nl
C এর মান পরিবর্তনের সাথে সাথে নকশায়ও পরিবর্তন আসে। মেনডেলব্রট সেটের সাথে জুলিয়া সেটের ঘনিষ্ঠ যোগাযোগ আছে। মেনডেলব্রট সেটের প্রতি প্রান্তে বিচিত্র নকশার জুলিয়া সেট ব্যবহার করা হয় যা মেনডেলব্রট জুমকে মনোমুগ্ধকর রুপে উপস্থাপন করে।
একটি সংক্ষিপ্ত মেনডেলব্রট জুমের ভিডিও দেয়া হলো। ফ্র্যাক্টালের যদি আপনার এটাই প্রথম পরিচয় হয়ে থাকে দেখে ফেলুন। আমি নিশ্চিত, আপনি মুগ্ধ হবেন।
ফ্র্যাক্টালের ব্যবহার
আধুনিক প্রযুক্তি জগতে ফ্র্যাক্টালের অবদান অবিস্মরণীয়। এর সবচেয়ে বেশি ব্যবহার লক্ষ্য করা যায় কম্পিউটার গ্রাফিক্সে। গ্রাফিক্সের কারসাজিতে যে দারুণ সব দৃশ্য বা নকশা তৈরী হয় তা মূলত ফ্র্যাক্টালের অবদান। দুর্দান্ত গতির আপনার প্রিয় ভিডিও গেমটি, প্রিয় কোনো সাইফাই সিনেমার কাল্পনিক জগত এসবই তৈরী করা সম্ভব হয়েছে ফ্র্যাক্টালের বদৌলতে।

স্টার ওয়ার্স সিরিজের ‘রৌগ ওয়ান:আ স্টার ওয়ার্স স্টোরি’ সিনেমায় ফ্র্যাক্টালের কারুকাজ; Source:milner’s blog
প্রকৃতি ও ফ্র্যাক্টাল
ফ্র্যাক্টাল ছড়িয়ে ছিটিয়ে আছে প্রকৃতির সবখানে। আকাশের মেঘ, সুউচ্চ পর্বত, সমুদ্র উপকূল, সাগরের ঢেউ, গাছের শাখা-প্রশাখা, ফুল, পাতা সবকিছুতে।

প্রকৃতির রাজ্যে ফ্র্যাক্টাল; Source:gaia.com
আপনি প্রকৃতির যেদিকেই তাকাবেন সেদিকেই ফ্র্যাক্টাল দেখতে পাবেন। ফ্র্যাক্টাল পাওয়া যায় আমাদের শরীরের রক্তনালীতে, মস্তিষ্ক, হৃদপিন্ড, ফুসফুসের মতো অঙ্গ-প্রত্যঙ্গেও। কম্পিউটারে তৈরীকৃত ফ্র্যাক্টালে মূলত প্রকৃতিরই অণুকরণ করা হয়। প্রকৃতির একই আকৃতির পুনরাবৃত্তি ও কম্পিউটারে তৈরী ফ্র্যাক্টালের পুনরাবৃত্তি পুরোপুরি একইরকম নয়। তারপরও ফ্র্যাক্টাল জ্যামিতির অণুপ্রেরণা প্রকৃতি থেকেই এসেছিল। ফ্র্যাক্টাল জ্যামিতি যে অনিন্দ্যসুন্দর প্রাকৃতিক দৃশ্য বা আকৃতিকে নকলই করে না, আমাদের শিশুসুলভ বিস্ময়কেও পুনরুজ্জীবিত করে।






.jpg?w=600)
