
মিশরীয়রা জ্ঞানচর্চায় সমসাময়িকদের চেয়ে অগ্রগামী ছিল এ কথা নিয়ে আপত্তি নেই ইতিহাসবিদদের। তাদের বিখ্যাত কীর্তি পিরামিডকে ঘিরে বেরিয়ে এসেছে তাদের জ্ঞানচর্চার বিভিন্ন দিক। গণিতে পিরামিড বা কোণকের আকৃতির রয়েছে বিশেষ সমাদর। কোণক বা পিরামিডের মাথা কেটে ফেললে যা পাওয়া যায়, তাকে গণিতের ভাষায় ফ্রাস্টাম বলা হয়।

পিরামিড নির্মাণের বিভিন্ন ধাপে মিশরীয়দের এই ফ্রাস্টামের আয়তন নির্ণয় করতে হতো। জ্ঞান বিজ্ঞানে উন্নত তৎকালীন মিশরীয়রা নিজেরাই ফ্রাস্টামের আয়তন নির্ণয়ের একটি সূত্র প্রতিষ্ঠা করে। সূত্রটি ছিল,
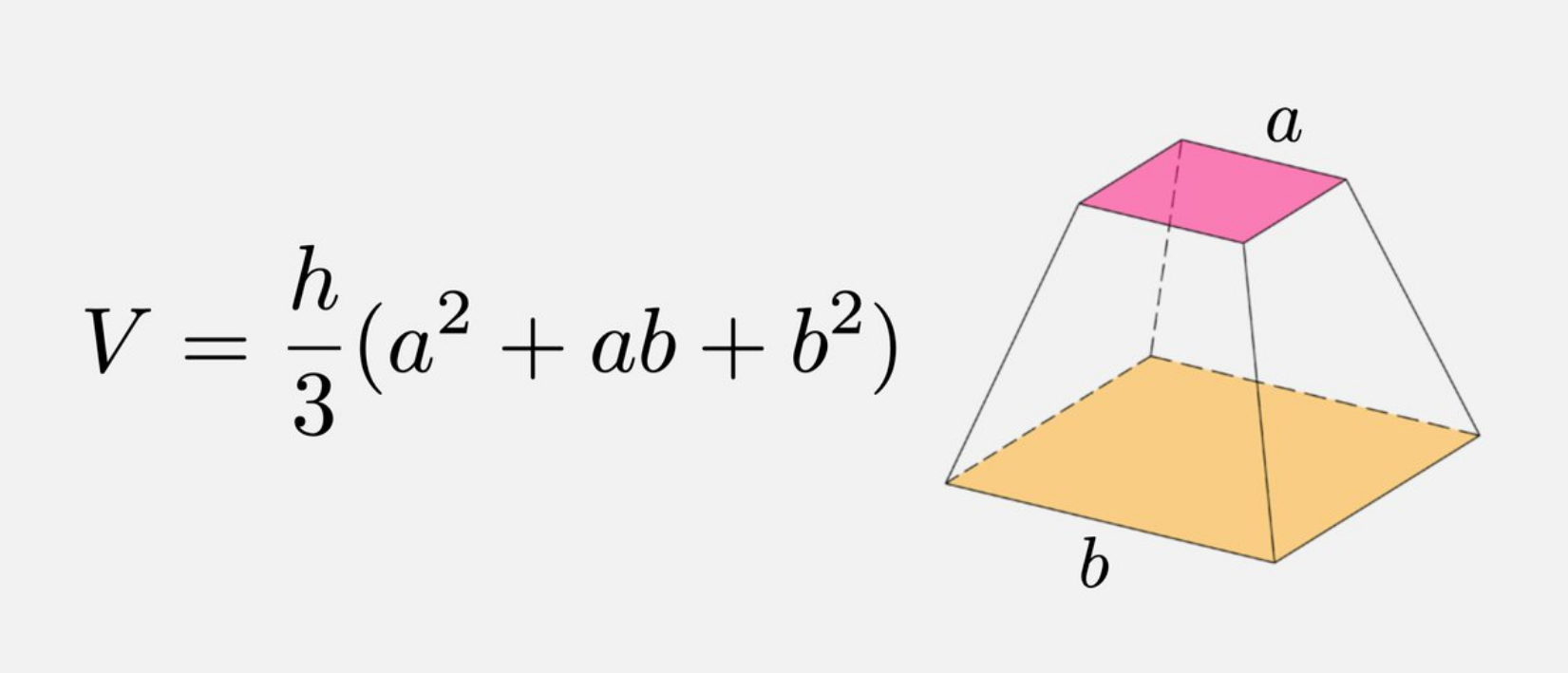
এখানে, a ও b দ্বারা যথাক্রমে শীর্ষবর্গের বাহু ও ফ্রাস্টামের ভূমির দৈর্ঘ্যকে বোঝানো হয়েছে। তবে একটি ফ্রাস্টামের উচ্চতা সরাসরি পরিমাপ করে তার আয়তন নির্ণয় করা বর্তমান সময়ে সহজসাধ্য হলেও তখন বেশ দুরূহ কাজ ছিল। তাই মিশরীয়রা তাদের সুবিধার্থে ফ্রাস্টামের আড়দৈর্ঘ্যের মান ব্যাবহার করে এর উচ্চতা নির্ণয় করত। সেক্ষেত্রে তাদের উচ্চতা নির্ণয়ের সূত্রটি ছিল:
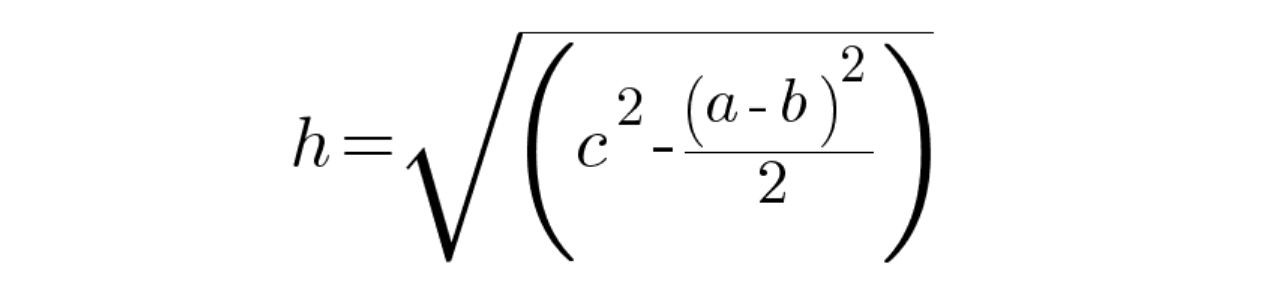
এখানে C হল আড় উচ্চতা।
এই সূত্রের দ্বারা পিরামিডের উচ্চতা নির্ণয়ে মিশরীয়রা একবার বেশ দ্বিধাদ্বন্দ্বের মধ্যে পড়ে যায়। পিরামিডটির ভূমি ছিল ২৮ মিটার, শীর্ষবর্গের বাহুর দৈর্ঘ্য ছিল ৪ মিটার ও আড়উচ্চতা ছিল ১৫ মিটার। সবগুলো মান সমীকরণে বসালে পাওয়া যায় উচ্চতা= √-৬৩। এই ঋণাত্মক সংখ্যার বর্গমূলটির মান কত হবে তা তখন কেউ জানত না। এই সমস্যা নিরসনে এগিয়ে আসেন আলেকজান্দ্রিয়ার বিখ্যাত গণিতবিদ হেরন। তিনি এই সমস্যা তুড়ি মেরে সমাধান করে বলেন, √৬৩ ও √-৬৩ আসলে একই জিনিস! এর ফলে ফ্রাস্টামের আয়তন নির্ণয়ে আর কোনো বাধা থাকল না। তবে সেটা আসলে ভুল ছিল। আর এই অতিসাধারণ সমাধানের মাধ্যমে হেরন জটিল সংখ্যা আবিষ্কারের সুবর্ণ সুযোগ হাতছাড়া করেছিলেন।

এমনকি মধ্যযুগের গণিতবিদরা ঋণাত্মক সংখ্যার বর্গমূল নির্ণয়কে অসম্ভব, কাল্পনিক বা মিথ্যা ধরে নেন। তবে আনুমানিক তৃতীয় শতাব্দীতে আলেকজান্দ্রিয়ার ডায়োফেন্টাস এবং ৮৫০ খ্রিস্টাব্দের কাছাকাছি সময়ে ভারতবর্ষের মহাবীর আচার্য ঋণাত্মক সংখ্যার বর্গমূলের তাত্ত্বিক সম্ভাবনার ধারণা পোষণ করেন।


১৪৫০ থেকে ১৬০০ খ্রিস্টাব্দের মধ্যবর্তী সময়ে দুইজন বিখ্যাত গণিতবিদ দেল ফেরো এবং কার্দানোর ঐকান্তিক প্রচেষ্টায় অবাস্তব সংখ্যার ধারণার পুনর্জন্ম ঘটে। আঠারো শতকে এসে অবাস্তব সংখ্যা তার কাঙ্ক্ষিত স্বীকৃতি লাভ করে। আর তখন থেকেই বাস্তব আর অবাস্তব সংখ্যার সমন্বয়ে জটিল সংখ্যা লেখার প্রচলন হয়।

কিন্তু জটিল সংখ্যার প্রকাশ নিয়ে গণিতবিদেরা বেশ দ্বিধাদ্বন্দ্বে পড়েন। কার্দানো সর্বপ্রথম বীজগণিতে জটিল সংখ্যার অবতারণা করেন। তিনি একে (a+√-b) আকারে প্রকাশ করতেন। তবে তিনি জটিল সংখ্যা প্রকাশের এই পদ্ধতি সম্পর্কে কোন সদুত্তর দিতে ব্যর্থ হন।
ঠিক তখনই দেবদূতের মত লিওনার্দো অয়লারের আগমন ঘটে। ১৭৭৭ সালে তিনিই সর্বপ্রথম একের ঋণাত্মক বর্গমূলকে ইংরেজি i অক্ষর দিয়ে প্রকাশ করেন। এছাড়াও তিনি জটিল সংখ্যাকে কার্তেসীয় স্থানাঙ্ক ব্যবস্থায় একটি বিন্দু দিয়ে প্রকাশ করারও ধারণা দেন। কিন্তু দুর্ভাগ্যবশত জটিল সংখ্যার মূল তত্ত্ব তিনি দিতে পারেননি। এর পেছনে অয়লারের ঋণাত্মক সংখ্যাভীতিই দায়ী বলে ধরা যায়।

বর্তমান সময়ে একটি সাধারণ সমীকরণ, যেমন: x+5=2 এর সমাধান আমরা চট করে করে ফেলতে পারি। কিন্তু অষ্টাদশ শতাব্দীর একজন ঝানু গণিতবিদ অয়লারের কাছে সেটাই ছিল অনেক কঠিন একটি সমীকরণ। কারণ তিনি ঋণাত্মক সংখ্যাকে বাস্তবে কিভাবে কাজে লাগাতে হয় জানতেন না। এমনকি একবার তিনি বলেছিলেন, ঋণাত্মক সংখ্যা অসীমের চেয়েও বেশি হতে পারে। তাই সাধারণ জনগণ, এমনকি সেকালের গণিতবিদেরাও ঋণাত্মক সংখ্যার সমস্যাকে এড়িয়ে যাওয়ার চেষ্টা করত।
তবে আজ থেকে পাঁচশত বছর আগে ইউরোপে এমন এক অভূতপূর্ব গাণিতিক সমস্যার উদ্ভব ঘটে, যার কারণে গণিতজ্ঞরা ঋণাত্মক সংখ্যাকে আর অবহেলা করতে পারলো না। সমস্যাটির মূল প্রবক্তা ছিলেন ইতালীয় গণিতবিদ দেল ফেরো। তিনি সেই সময়ে ত্রিঘাত সমীকরণের সমাধানের চেষ্টা করছিলেন। এর সাধারণ রূপটি হল (ax3+bx2+cx+d=0)। দেল ফেরো এই সাধারণ সমীকরণে কিছুটা পরিবর্তন আনেন। তিনি সমীকরণে x এর দ্বিঘাত অংশটি বাদ দেন এবং d অর্থাৎ ধ্রুবক অংশটির মান ঋণাত্মক ধরে নেন। উল্লেখ্য, কোনো ত্রিঘাত সমীকরণে দ্বিঘাত পদ অনুপস্থিত থাকলে তাকে ডিপ্রেসড ত্রিঘাত সমীকরণ বলে। কিন্তু আগেই বলা হয়েছে, মানুষজন তখনও ঋণাত্মক সংখ্যাকে বাঁকা চোখে দেখত। তাই তিনি চালাকি করে সমীকরণটিকে একটু সাজিয়ে গুছিয়ে লেখেন ax3+cx= d, যেখানে c এবং d উভয়েই ধনাত্মক পূর্ণ সংখ্যা। এরপর তিনি x এর মান বের করার কাজে লেগে পড়েন। অনেক হিসাব নিকাশের পর দ্বিঘাত সমীকরণের ন্যায় তিনি তার তৈরিকৃত সমীকরণের একটি সাধারণ সমাধান বের করেন। তবে দেল ফেরো সেই সমাধানটি লোকচক্ষুর আড়ালে গোপন রেখেছিলেন। অবশেষে মৃত্যুশয্যায় তার শিষ্য অ্যান্টোনিও ফোইরকে তিনি সেই গুপ্ত সমাধানের কথা বলে দেন।
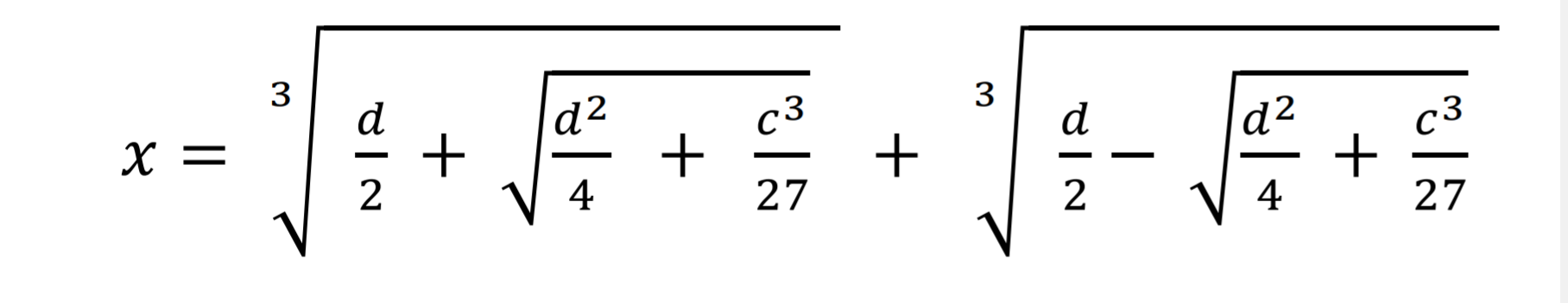
ফোইর সেই সমাধানের খোঁজ পাওয়ার পর তার বহুদিনের পুরনো শত্রু বিখ্যাত ইতালীয় গণিতবিদ ফনটানা টারটাগলিয়াকে হারানোর জন্য দৃঢ়প্রতিজ্ঞ হয়ে ওঠেন। তিনি দেল ফেরোর সেই গাণিতিক সমস্যা সমাধানের জন্য টারটাগলিয়াকে চ্যালেঞ্জ ছুঁড়ে দেন।

টারটাগলিয়াও কম যাননি, তিনিও সেই চ্যালেঞ্জ গ্রহণ করেন। সমাধানের বেঁধে দেয়া সময়সীমার একেবারে দ্বারপ্রান্তে তিনি সেই সমস্যার সমাধানই শুধু বের করেননি, উল্টো ফোইরকেই পাল্টা চ্যালেঞ্জ ছুঁড়ে দেন। কারণ তিনি ফোইর তথা দেল ফেরোর সমাধানের একটি লক্ষণীয় ত্রুটির খোঁজ পান। তিনি গাণিতিকভাবে দেখান, a, c এবং d এর কিছু সুনির্দিষ্ট মানের জন্য (যেমন: a=1, c=15, d=4) ফোইরের সমাধান যুক্তিযুক্ত হয় না। কারণ সেক্ষেত্রে ঋণাত্মক সংখ্যার বর্গমূল বের করার প্রয়োজন পড়ে।
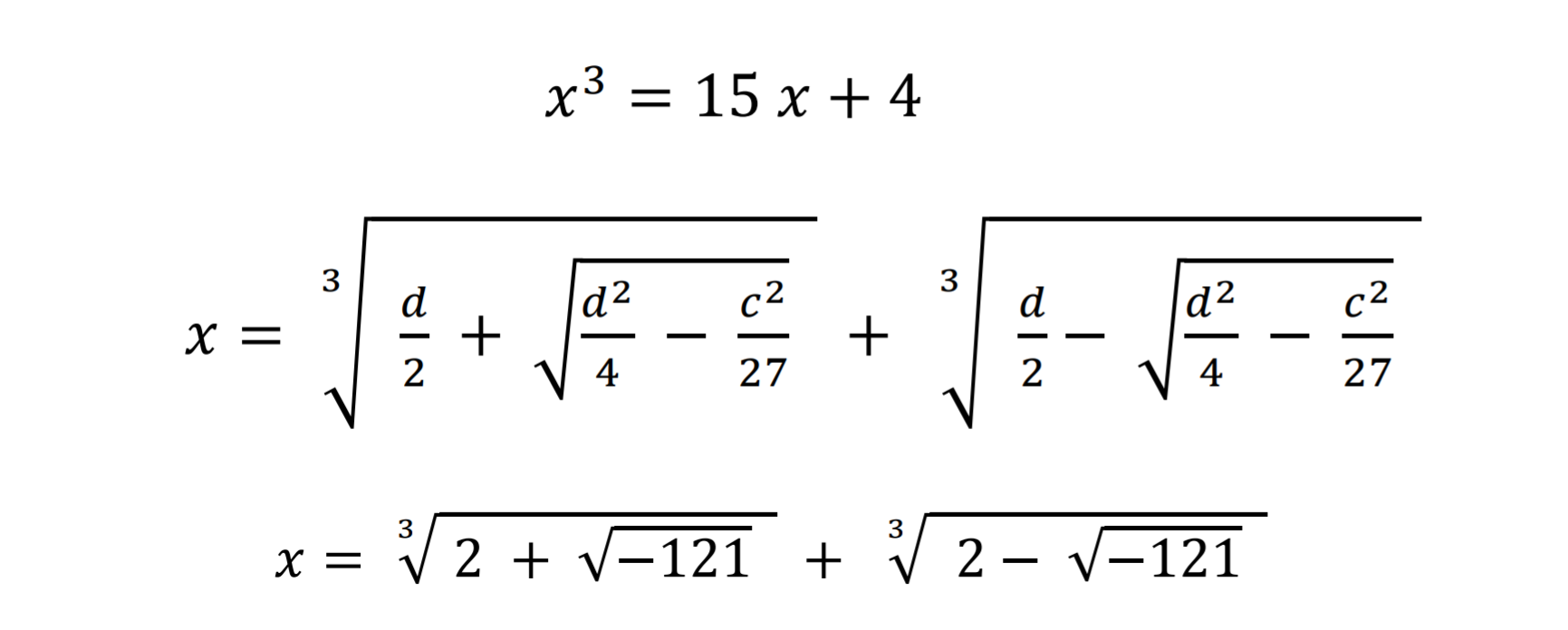
বিখ্যাত গণিতবিদ কার্দানো সমস্যাটি সম্পর্কে জানার পর সেটি সমাধানে সচেষ্ট হন। তিনি ঋণাত্মক সংখ্যার বাস্তব প্রয়োগের একটি নিয়ম আবিস্কার করলেও আলোচিত সমস্যাটির সমাধানে বেশি দূর যেতে পারেননি। কার্দানোর মৃত্যুর পর তাঁর ছাত্র বোম্বেলি সমস্যাটি নিয়ে নতুনভাবে গবেষণা শুরু করেন।
বোম্বেলি চিন্তাধারায় তাঁর পূর্বসূরিদের চেয়ে ভিন্ন ছিলেন। তিনি ভাবলেন, ধনাত্মক বা ঋণাত্মক সংখ্যার সাহায্যে সমাধান না পাওয়া গেলে অন্য কোনো সংখ্যা আছে যেটা এই সমীকরণকে সিদ্ধ করবে। তাই সকলে ঋণাত্মক সংখ্যার বর্গমূলকে অগ্রাহ্য করলেও তিনি একে সংখ্যা হিসেবে স্বীকৃতি দেন। তবে তিনি ভিন্ন কোনো সংখ্যা বা প্রতীকের বদলে √-1 কে সংখ্যার মর্যাদা দেন। তখন এক নতুন সমস্যার জন্ম হয়। √-1 কি আসলে বাস্তব সংখ্যা? তাই বোম্বেলির পক্ষে সংখ্যা রেখায় নতুন আবিষ্কৃত সংখ্যার স্থান সংকুলান করাই ছিল অনেক বড় দুরূহ কাজ। তিনি জানতেন, এর আগেও সংখ্যা রেখায় বেশ কয়েকবার পরিবর্তন আনা হয়েছে। সময় এসেছে আবার এক বৈপ্লবিক পরিবর্তনের। তবে এর আগে তিনি কার্দানোর সমীকরণকে আরও সরলভাবে উপস্থাপনের চেষ্টা করেন।

গাণিতিকভাবে তিনি দেখান, টারটাগলিয়ার প্রস্তাবিত সমস্যাটিতে বিদ্যমান সমাধানটিতে যে দুইটি পদ রয়েছে, তাদের যোগ করলে √-1 সম্বলিত পদটি আর থাকে না। তখন পুরো সমাধানটি বাস্তব সংখ্যা হয়ে যায়। তিনি তখন দুইটি পদকে নিম্নোক্ত উপায়ে সংজ্ঞায়িত করেন।
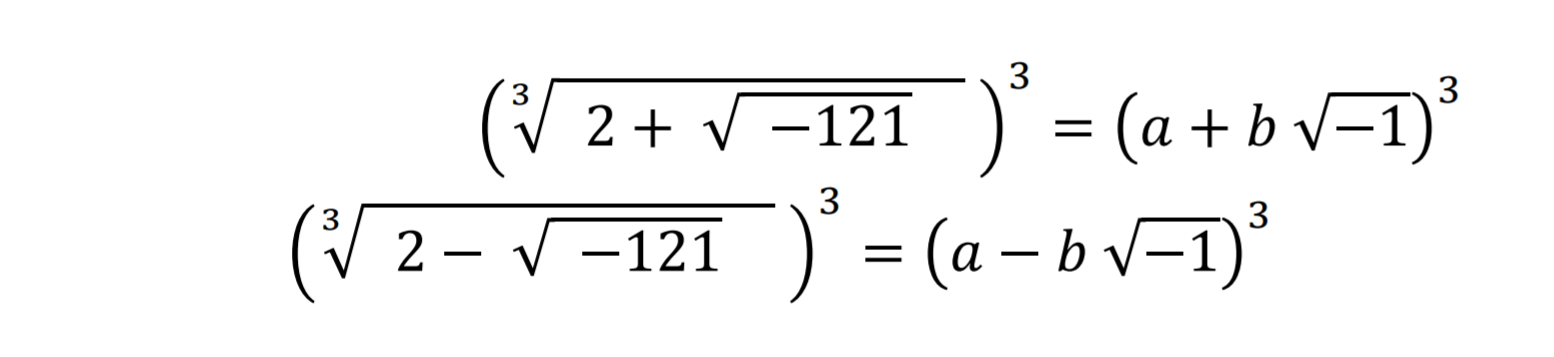
এরপর তিনি সমীকরণটি থেকে ঘনফল মুক্ত করেন এবং কতিপয় হিসাব করে সর্বশেষে নিচের দুইটি সমীকরণে উপনীত হন।
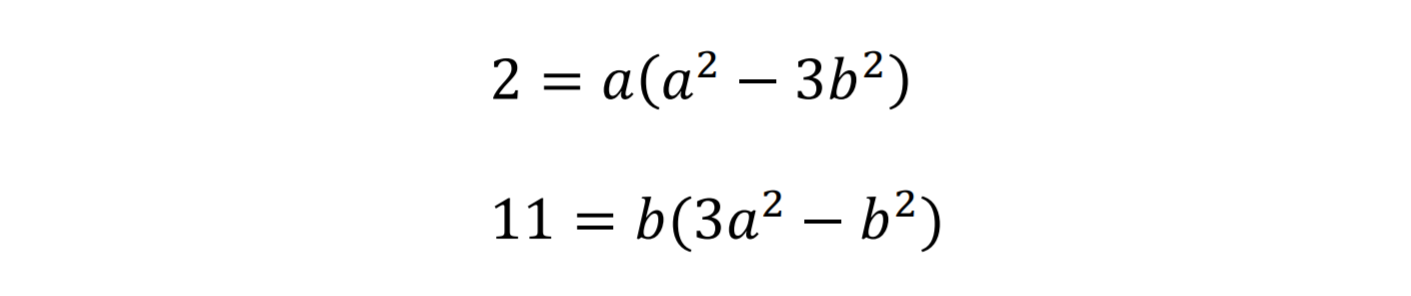
উপরের দুইটি সমীকরণ সমাধান শেষে তিনি পান a=2 এবং b=1। পরবর্তীতে টারটাগলিয়ার সমীকরণে a এবং b এর মান বসালে সমাধান পাওয়া যায় 4। আর এরই মাধ্যমে কার্দানোর সমীকরণের মূল সমস্যা দূরীভূত হয়। তবে সেক্ষেত্রে শর্ত একটাই। √-1 কে সংখ্যার মর্যাদা দিতে হবে। কিন্তু স্বাভাবিক চিন্তাধারায় সংখ্যারেখার কোথাও তাকে বসানো যাচ্ছিল না। কারণ বাস্তব জগতে √-1 কে কেউ সংখ্যা হিসেবে কল্পনা করতে পারছিল না। সেই জন্যই একে কাল্পনিক বা Imaginary সংখ্যা হিসেবে অভিহিত করা হয়। তবে প্রকৃত অর্থে √-1 একটি সংখ্যা। জটিল সংখ্যার সংখ্যারেখায় এর অস্তিত্ব রয়েছে। এমনকি এর নিজস্ব প্যাটার্নও রয়েছে।
এই ধারণাটি এসেছিল বোম্বেলির সমাধানেরও ১০০ বছর পরে। ১৭৭৭ সালে সুইজারল্যান্ডের গণিতবিদ লিওনার্দো অয়লার ঋণাত্মক সংখ্যার বর্গমূলকে একটু বদলে সংখ্যাটির বর্গমূলকে বাস্তব বা ধনাত্মকরুপে রেখে তার সাথে -1 এর বর্গমূল গুণ করে প্রকাশ করেন (যেমন:√-63= √63*√-1)। পরবর্তীতে সেটা আরও সংক্ষেপে i দ্বারা চিহ্নিত করেন তিনি (√63 i)। যার ফলে বাস্তব আর অবাস্তব অর্থাৎ √-1 এর বাস্তব সহগের সমন্বয়ে গড়ে ওঠে এক অভিনব নতুন সংখ্যা পদ্ধতি (যেমন: 6+3i)। যার নাম রাখা হয় জটিল সংখ্যা। এমনকি পৃথিবীর সুন্দরতম সমীকরণ হিসেবে পরিচিত অয়লারের সমীকরণটিও i সমন্বয়ে সাজানো।
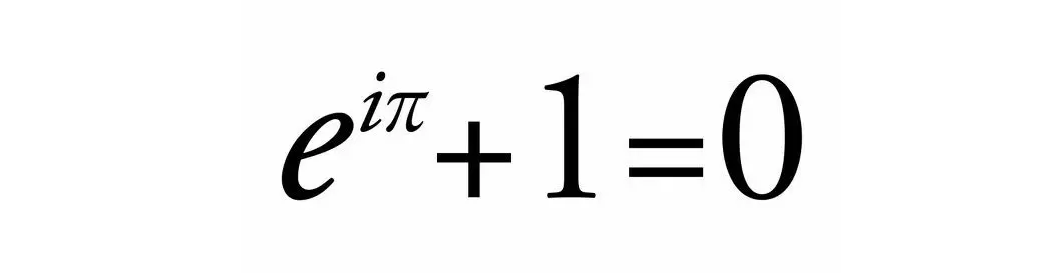
কিন্তু i কে সংখ্যারেখায় বসানোর চিরায়ত সমস্যার তখনও কোনো সুরাহা হয়নি। সমস্যাটিকে অন্যভাবে বললে বলা যায়, এমন একটি সংখ্যা খুঁজে বের করতে হবে যাকে দুইবার গুণ করলে একটি ঋণাত্মক সংখ্যা পাওয়া যায়। কিন্তু বাস্তব সংখ্যারেখায় তেমন কোনো সংখ্যাই পাওয়া যাচ্ছিল না। উদাহরণস্বরূপ, ৩ সংখ্যাটিকে ধরা যায়। ৩ এর সাথে ৩ গুণ করলে ৯ পাওয়া যায়।

আবার -৩ এর সাথে -৩ গুণ করলেও ৯ পাওয়া যায়।
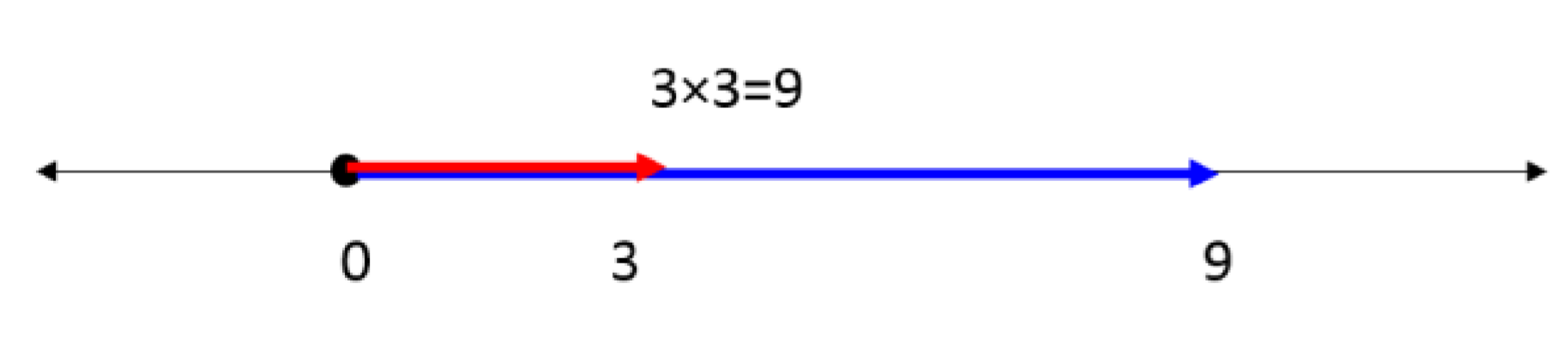
তার মানে সংখ্যারেখায় ডান বা বাম যেদিক থেকেই শুরু করা হোক না কেন, ফলাফল ১৮০ ডিগ্রি পরিবর্তন হয়ে সবসময় সংখ্যারেখার ধনাত্মক দিকেই বিরাজ করবে।
এই সমস্যা সমাধানে গণিতবিদেরা এমন এক সংখ্যার ধারণা প্রবর্তন করেন, যে সংখ্যা দুইবার গুণ করলে ফলাফল ১৮০ ডিগ্রি না ঘুরে ৯০ ডিগ্রী ঘুরবে। অবাস্তব সংখ্যাগুলো ঠিক এভাবেই কাজ করে। বাস্তব সংখ্যার সূচক বৃদ্ধির ফলে এর মান বাড়ে। কিন্তু অবাস্তব সংখ্যা তথা i এর সূচক বা ঘাত বাড়ালে এর মান বাড়ে না, কিন্তু এর মানের একটি মজার বিন্যাস তৈরি হয়। প্রতি ৪ বার গুণনের পর একই সংখ্যার পুনরাবৃত্তি ঘটতে থাকে।
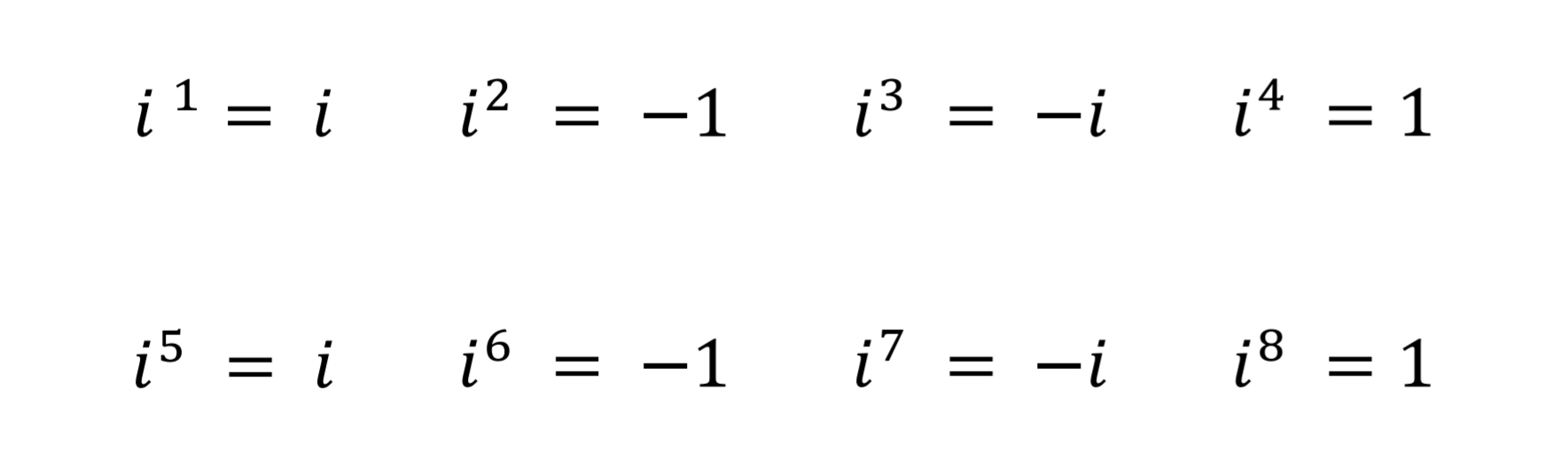
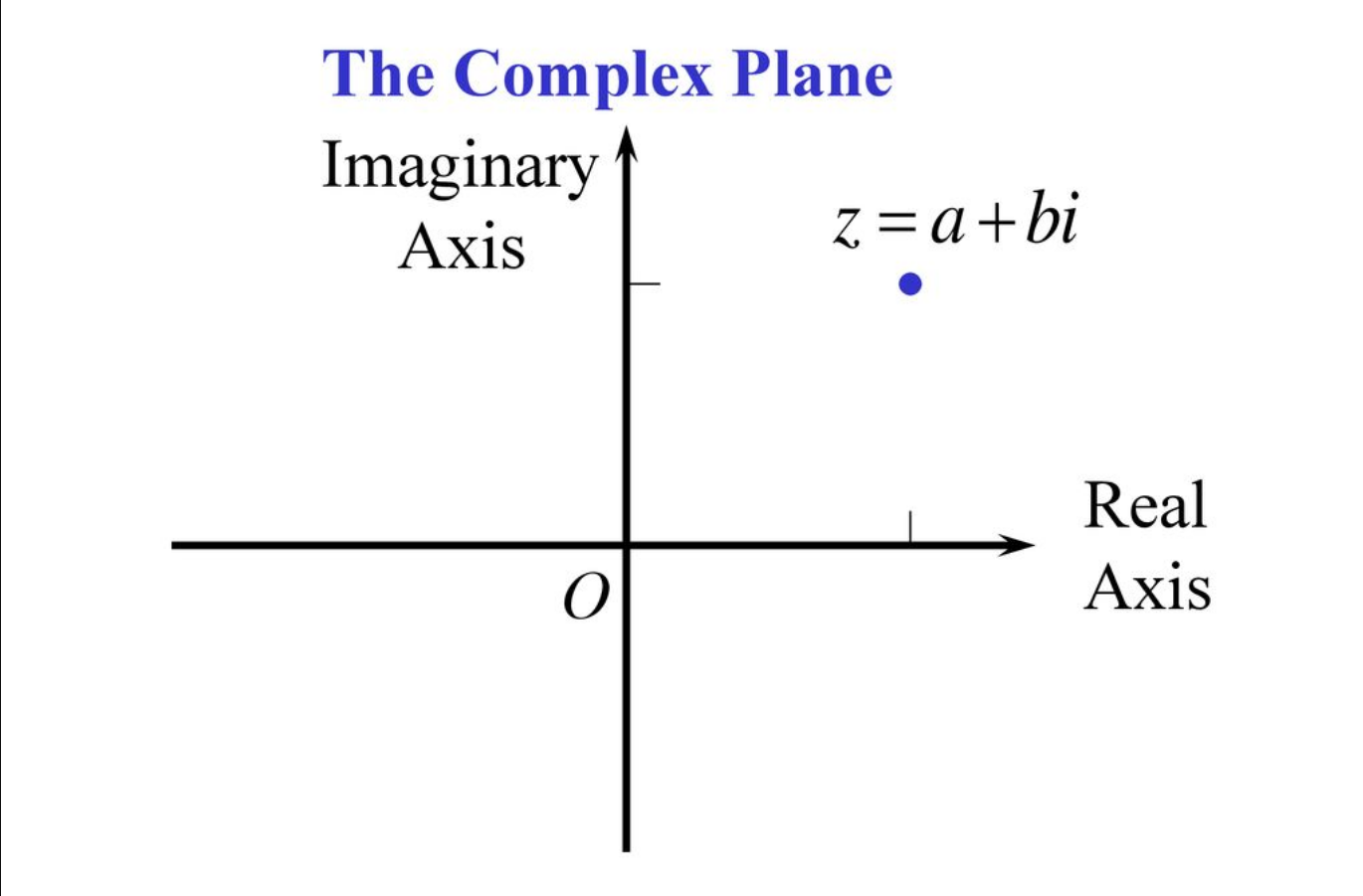
আর এভাবেই জটিল সংখ্যা রেখার সূচনা হয়। যেখানে বাস্তব সংখ্যারেখার সাথে সমকোণে অবাস্তব বা কাল্পনিক সংখ্যারেখার সংযোজন ঘটে। এর মাধ্যমে দ্বিমাত্রিক সংখ্যারেখার উদ্ভব হয়। আর সেই সাথে সংখ্যা নিয়ে মানুষের মৌলিক ধ্যান ধারণার আমূল পরিবর্তন ঘটে।
তবে যদি কোনো তড়িৎ প্রকৌশলী বলে j=√-1, তবে বিচলিত হবার কোন কারণ নেই। কারণ তড়িৎবিষয়ক বিভিন্ন সমস্যা সমাধানে তারা i দিয়ে তড়িৎপ্রবাহকে নির্দেশ করে। (উল্লেখ্য, ১৮৯৪ সাল পর্যন্ত তড়িৎ প্রকৌশল বিষয়ক এক জার্নালে তড়িৎ প্রবাহকে C দিয়ে প্রকাশ করা হত। এরপর তারা প্রথমে ক্যাপাসিটর বা ধারকের নাম C দিয়ে প্রকাশের সিদ্ধান্ত নেয়। আর তড়িৎ প্রবাহের সংকেত হিসেবে Cu (Current শব্দের প্রথম দুইটি অক্ষর) ব্যবহারের জন্য নির্বাচিত করে। কিন্তু তখন রসায়নবিদরা এর বিরোধিতা করে। কারণ পর্যায় সারণিতে কপার বা তামা-কে Cu দিয়ে প্রকাশ করা হয়। সকল ধরনের সংশয় দূর করার লক্ষ্যে তড়িৎ প্রবাহের একক যার নামে রাখা হয়েছে সেই ফ্রেন্স বিজ্ঞানী আন্দ্রে মেরি অ্যাম্পিয়ারের সম্মানার্থে তড়িৎ প্রবাহ ঘনত্বের ফ্রেন্স অনুবাদ ‘intensité du courant’ -এর আদ্যাক্ষর i-কে তড়িৎপ্রবাহের প্রতীক হিসেবে নির্ধারণ করা হয়)। তাই হিসাবের গণ্ডগোল এড়াতে তারা অবাস্তব সংখ্যাকে j দিয়ে প্রকাশ করে থাকে।


.jpeg?w=600)




