ব্যারোমিটারের সেই বিশ্ববিখ্যাত সমস্যা

কোপেনহেগেন বিশ্ববিদ্যালয়ে একবার পদার্থবিজ্ঞান পরীক্ষার প্রশ্নে এই সমস্যাটি এসেছিল। একটি ব্যারোমিটারের সাহায্যে কীভাবে একটি সুউচ্চ ভবনের উচ্চতা পরিমাপ করবে? দেখতে একদমই নিখাদ ও সাদামাটা মনে হলেও প্রশ্নটিতে বেশ কিছু সীমাবদ্ধতা লুকিয়ে ছিল। প্রশ্নকর্তার প্রত্যাশা ছিল অনেকটা এমন- ছাত্ররা প্রথমে ভবনের সবচেয়ে উঁচুতে ব্যারোমিটারের চাপ নির্ণয় করবে এবং পরে ভবনের সবচেয়ে নিচুতে (ভূমি) ব্যারোমিটারের চাপ নির্ণয় করবে। উপরের চাপ এবং নিচের চাপের পার্থক্য থেকে হিসাব নিকাশ করে ভবনের উচ্চতা বের করা যাবে।

কিন্তু এক ছাত্র এই পদ্ধতির ধারে কাছেও না গিয়ে অনেকটা রসিকতা করেই লিখলো- প্রথমে ব্যারোমিটারটিকে ভবনের ছাদে নিয়ে যেতে হবে। তারপর এর সাথে লম্বা একটি দড়ি বাধতে হবে। বাধার পর একে ছাদ থেকে ধীরে ধীরে ভূমিতে নামাতে হবে। ভূমি স্পর্শ করার পর দড়ির দৈর্ঘ্য ও ব্যারোমিটারের দৈর্ঘ্য যোগ করলে যে ফল আসবে তা-ই হবে ভবনটির উচ্চতা।

ছাত্র তো উত্তর দিয়ে দিলো, কিন্তু শিক্ষক তো তাতে কোনোক্রমেই সন্তুষ্ট নয়। এমন দায়সারা অলস উত্তরে শিক্ষক তাকে শূন্য দিয়ে ফেল করিয়ে দিলেন। এই ফলাফলে ছাত্র আবার অসন্তুষ্ট হয়ে গেল। ছাত্রটি বিশ্ববিদ্যালয়ের কাছে আবেদন করলো যে তার উত্তরটি কোনো দিক থেকেই ভুল ছিল না, তার উত্তরের যেন সঠিক মূল্যায়ন করা হয়। ছাত্রের আবেদন আমলে নিয়ে বিশ্ববিদ্যালয় কর্তৃপক্ষ নিরপেক্ষ মূল্যায়নের জন্য অন্য একজন বিচারকের শরণাপন্ন হলেন। বিচারকের নাম অ্যালেকজান্ডার ক্যালান্ড্রা (১৯১১ – ২০০৬), তিনি পদার্থবিজ্ঞানের অধ্যাপক এবং পদার্থবিজ্ঞান সম্পর্কিত কিছু বইয়ের লেখক।

সাধারণ ব্যারোমিটার; ছবি: Ballyraine

বিচারক দেখলেন উত্তরকে তো ভুল বলা যায় না, কারণ যা লিখেছে তা একদিক থেকে সঠিক। আবার সঠিক বলে নাম্বারও দেয়া যায় না, কারণ এখানে পূর্ণ নাম্বার দেয়া হলে সেটি তার গ্রেড উন্নয়নে প্রভাব রাখবে। ভালো গ্রেড তারাই পাবার দাবী রাখে যাদের সংশ্লিষ্ট বিষয়ের উপর যথেষ্ট দখল আছে। পরীক্ষার মাধ্যমে দখল থাকার ব্যাপারটি যাচাই করা যায়। কিন্তু ছাত্রটির এমন উত্তরে তো প্রমাণ হয় না যে পাঠ্যক্রমের বিষয়গুলো তার দখলে আছে। এখানে তো বিষয়ের সাথে সংশ্লিষ্ট পদার্থবিজ্ঞানের কোনো জ্ঞানের উল্লেখ নেই। তাকে কীভাবে পূর্ণ নাম্বার দেয়া যায়?

তিনি সিদ্ধান্ত নিলেন উত্তরের জন্য ছাত্রটিকে আরেকবার সুযোগ দেবেন। প্রশ্নকর্তা শিক্ষকও তাতে সম্মতি দিলেন। কিন্তু এরপরে ছাত্রটি যা করলো তা আরো অবাক করার মতো।

বিচারক তাকে ছয় মিনিট সময় দিলেন। এই সময়ের মাঝে ঐ প্রশ্নটির উত্তর দিতে হবে। পাশাপাশি সতর্কও করে দিলেন, উত্তর অবশ্যই পদার্থবিজ্ঞান সংশ্লিষ্ট হতে হবে। ছয় মিনিটের প্রথম পাঁচ মিনিট কোনো কিছু না করেই কেটে গেলো। ছাত্রটি তখনও ভ্রু কুচকে চিন্তাই করে যাচ্ছিল। মূল্যায়নকারী বিচারক তখন হতাশ হয়ে জানতে চাইলেন না পারলে উত্তর দেবার চেষ্টা ছেড়ে দেবে কিনা? ছাত্রটি বলে না, ছাড়বে না। তার কাছে পদার্থবিজ্ঞান সংশ্লিষ্ট বেশ কয়েকটি যুক্তিযুক্ত উত্তর আছে কিন্তু কোনটি বললে সবচেয়ে ভালো হবে তা বুঝে উঠতে পারছে না। এ কথা শুনে বিচারক নড়েচড়ে বসলেন এবং যেকোনো একটি উত্তর শুনতে চাইলেন।

ছাত্র উত্তর দিলো- প্রথমে ব্যারোমিটারটিকে ভবনের সর্বোচ্চ বিন্দুতে নিয়ে যাবেন। এরপর সাবধানে ছাদের কিনারে গিয়ে সেখান থেকে ব্যারোমিটারটিকে ভূমির দিকে ছেড়ে দেবেন। একটি স্টপওয়াচের সাহায্যে পরিমাপ করবেন নিচে পড়তে এর কত সময় লেগেছে। সময়ের পরিমাণ পাওয়া গেলে সেখান থেকে h = ut + 1/2(gt^2) সূত্র ব্যবহার করে ভবনের উচ্চতা (h) বের করা যাবে।

যদিও এই উত্তরটি প্রত্যাশিত উত্তরের সাথে মিলে না তারপরেও মূল্যায়নকারী এ উত্তর শুনে তাকে প্রায় সম্পূর্ণ নাম্বার প্রদান করলেন। তিনি রুম থেকে বেরিয়ে যাবেন এমন সময় ছাত্রের কাছ থেকে ডাক শুনতে পান। ছাত্র জানায় তার কাছে আরো কিছু উত্তর আছে। বিচারক তার উত্তরগুলো শুনতে চাইলে সে গড়গড় করে বলতে থাকে।

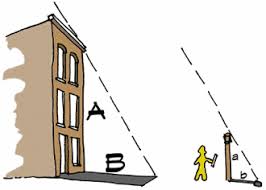
ব্যারোমিটারের সাহায্যে আরো অনেক উপায়েই ভবনের উচ্চতা পরিমাপ করা যাবে। যেমন, সূর্যালোকিত দিনে আপনি একটি ব্যারোমিটারের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য মাপতে পারেন। তারপর ভবনের ছায়ার দৈর্ঘ্য মেপে অনুপাতের সূত্র প্রয়োগ করে সহজেই ভবনের উচ্চতা পরিমাপ করতে পারেন।

ছবি: Mr. Gresser’s

পরিমাপের একদম সাধারণ ধারণার মাধ্যমেও ভবনের উচ্চতা নির্ণয় করা সম্ভব। তার জন্য আগে ব্যারোমিটারের দৈর্ঘ্য মাপতে হবে। এরপর সিঁড়ি দিয়ে উঠার সময় দেয়ালে ব্যারোমিটারের সমান দৈর্ঘ্যে একটি একটি করে দাগ কেটে কেটে উপরে উঠতে হবে। পরে সবগুলো দৈর্ঘ্যকে একত্রে যোগ করে সহজেই পাওয়া যাবে ভবনের উচ্চতা।

পদার্থবিজ্ঞান সংশ্লিষ্ট আরো বাস্তবধর্মী উত্তর চাইলে এক কাজ করতে পারেন। ব্যারোমিটারটিকে একটি তন্তুতে বেঁধে সরল দোলকের মতো করে নিন। তারপর একে ভবনের উঁচু ছাদে এবং ভূমিতে দুলিয়ে দুই স্থানের অভিকর্ষজ ত্বরণ (g) নির্ণয় করতে পারেন। দুই রকম অভিকর্ষজ ত্বরণের পার্থক্য থেকে হিসাব নিকাশ করে ভবনের উচ্চতা বের করা সম্ভব।

এমনিতে যদি ‘পদার্থবিজ্ঞানের নিয়ম থাকতেই হবে’ এমন বাধ্যবাধকতা না থাকে তাহলে আরো বেশ কিছু উপায় আছে ভবনের উচ্চতা মাপার। যেমন, ব্যারোমিটারটিকে হাতে নিয়ে নিচতলায় ম্যানেজারের কাছে যেতে পারেন, যিনি ভবনটি রক্ষণাবেক্ষণ করছেন। তার রুমে নক করলে তিনি কারণ জানতে চাইলে বলবেন- আমার হাতে খুব চমৎকার ও দৃষ্টিনন্দন একটি ব্যারোমিটার আছে। আপনি যদি এই ভবনটির উচ্চতা কত তা আমাকে বলে তাহলে ব্যারোমিটারটি আপনাকে দিয়ে দেব। এভাবে ব্যারোমিটারের সাহায্যে জানতে পারবেন উচ্চতা।

এই পর্যায়ে বিচারক ছাত্রটির কাছে জানতে চাইলেন সে আসলেই প্রাসঙ্গিক উত্তরটি জানে নাকি জানে না? ছাত্র জানায় সে আসলে জানে। কিন্তু সে এমন করেছে কারণ হাই স্কুল ও কলেজের শিক্ষকরা যেভাবে বৈজ্ঞানিকভাবে চিন্তা করা সম্পর্কে পড়িয়েছে তাতে সে বিরক্ত হয়ে গেছে। বিজ্ঞানের ইতিহাসে এই ঘটনাটি অনেক বিখ্যাত এবং এটি ‘ব্যারোমিটার প্রবলেম’ নামে পরিচিত।

আধুনিক ব্যারোমিটার; ছবি: Vavasseur Antiques

নিলস বোর এলো কোথা থেকে

অনেকে বলে থাকে ব্যারোমিটার প্রবলেম ঘটনার ছাত্রটি আসলে পদার্থবিজ্ঞানে নোবেলজয়ী বিজ্ঞানী নিলস বোর। কিন্তু আসলে এই ঘটনাটির সাথে নিলস বোরের কোনো সম্পর্ক নেই। স্নোপস ডট কমের এক অনুসন্ধানে বেরিয়ে এসেছে পদার্থবিজ্ঞানের এই ‘উপকথা’টির প্রথম দেখা পাওয়া যায় ১৯৫৮ সালে রিডার ডাইজেস্ট ম্যাগাজিনের একটি সংখ্যা থেকে। পরবর্তীতে ১৯৬১ সালে বিচারক ড. অ্যালেকজান্ডার ক্যালান্ড্রা তার বই The Teaching of Elementary Science of Mathematics-এ ঘটনাটির উল্লেখ করেন। আরো পরে ১৯৬৮ সালে স্বতন্ত্র প্রবন্ধ হিসেবে স্যাটারডে রিভিউতে প্রকাশিত হয়। এরপর এটি অনেকবার অনেক সাময়িকীতে পুনঃপ্রকাশিত হতে থাকে। কিন্তু বাস্তবতা হচ্ছে এর অনেক অনেক আগেই নিলস বোরের ছাত্রত্ব শেষ হয়ে গেছে। এমনকি ১৯২২ সালে তিনি পদার্থবিজ্ঞানে নোবেল পুরষ্কারই পেয়ে গেছেন।

নিলস বোর; ছবি: উইকিমিডিয়া কমন্স

বিচারক অ্যালেকজান্ডার ক্যালান্ড্রা এই ঘটনাটি প্রথম পুরুষ (First person)-এ উল্লেখ করেন। ব্যারোমিটার প্রবলেমের ঘটনাটি উনার জন্মই হয়েছে ১৯১১ সালে। অন্যদিকে ১৯২২ সালে বোর পদার্থবিজ্ঞানে নোবেল পুরষ্কারই পেয়ে গেছেন। সেই হিসেবে সহজেই অনুমান করা যায় ঘটনার সাথে নিলস বোরের কোনো সম্পর্ক নেই। বিচারক শিক্ষকের চেয়ে নিলস বোরের বয়স বেশি। বোরের জন্ম ১৮৮৫ সালে। সম্ভবত ঘটনাটিকে একটু নাটকীয় করার জন্য ইন্টারনেট জগতে ছাত্রটিকে বোর বলে দাবী করা হয়। এই ঘটনাটি সত্য, কিন্তু ছাত্রটি আর যে-ই হোক অন্তত নিলস বোর নয়।

এই ঘটনাটি আমাদের পরীক্ষার প্রশ্নের সীমাবদ্ধতাগুলো তুলে ধরে। প্রশ্নকর্তার উচিৎ প্রশ্নের মাঝে কাঙ্ক্ষিত উত্তর দেবার প্রক্রিয়া সম্পর্কে স্পষ্ট করে বলা। যেমন সেখানে ব্যারোমিটারের পাশাপাশি বায়ুচাপ ব্যবহার করে উচ্চতা বের করার কথা উল্লেখ করে দিলে প্রশ্নের সীমাবদ্ধতা থাকতো না।

পাশাপাশি আরো একটি দিক সম্বন্ধে আঙুল তুলে ধরে। পরীক্ষায় কিছু কিছু শিক্ষক তাদের পছন্দমতো পদ্ধতিতে উত্তর না দিলে নম্বর কেটে দেয়। বিশেষ করে বাংলাদেশে গণিতের বেলায় এমনটি বেশি হয়। উত্তরে ভুল না থালেও উত্তর দেবার পদ্ধতিতে ভিন্নতা থাকলেই নাম্বার কাটা। অথচ উত্তরপ্রদানকারী সম্পূর্ণ নম্বর পাবার যোগ্য।

ব্যারোমিটার কী?

আবহাওয়ার খুব গুরুত্বপূর্ণ একটি যন্ত্র। এর সাহায্যে বায়ুর চাপ পরিমাপ করা হয়। আবহাওয়া পরিবর্তনের সাথে বায়ুর চাপের ভিন্নতা তৈরি হয়। বায়ুতে জলীয় বাষ্পের পরিমাণ বাড়লে বা কমলে বাতাসের চাপ কমে বা বেড়ে যায়। চাপের তারতম্য হলে তা ব্যারোমিটারে ধরা পড়ে। বায়ুতে নিম্নচাপ তৈরি হলে বৃষ্টি হবার প্রবল সম্ভাবনা থাকে। সেজন্য একে আবহাওয়ার পূর্বাভাস দেবার জন্য ব্যবহার করা হয়ে থাকে।

ফিচার ছবি- Vavasseur Antiques