শূন্যের ইতিহাস: শূন্য যেভাবে সংখ্যা হিসেবে প্রতিষ্ঠিত হলো

শূন্য মানে ‘কিছু না’ আবার শূন্যই একটি সংখ্যা। সেই কিছুই না থেকে কি কখনো কিছুর উৎপত্তি হতে পারে? কিংবা সেই ‘কিছুই না’ কি একটি সংখ্যা হতে পারে। কিছু না মানে তো ‘কিছুই নেই’। ১ মানে একটি জিনিস, ২ মানে দুটি, কিন্তু শূন্য মানে কী? যা নেই তা আবার সংকেত দিয়ে প্রকাশ করার কী দরকার? এমন হাজারো প্রশ্ন উঁকি দিয়ে গেছে প্রাচীন সভ্যতার বাঘা বাঘা সব গণিতবিদের মাথায়। বাহ্যত, শূন্যের কোনো প্রয়োজন নেই। কিন্তু শূন্য ছাড়া আমরা অচল। সেই রহস্যময় শূন্যের উৎপত্তি কবে হলো, কে বা কোন সভ্যতা প্রথম শূন্য ব্যবহার করেছে? নিশ্চয়ই মনে এমন প্রশ্ন উঁকি দেয় আমার মতো আপনারও? চলুন তাহলে আপনাকে প্রথমে নিয়ে যাই সুমেরীয় সভ্যতায়।

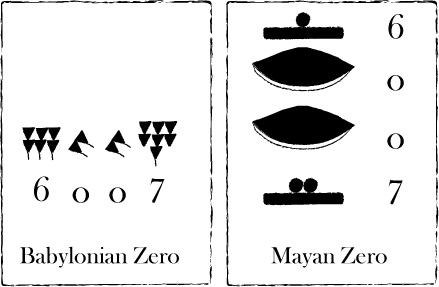
৪,০০০-৫,০০০ বছর আগে সুমেরীয়রা প্রথম গণনা ব্যবস্থার প্রচলন শুরু করে। তাদের গণনা ব্যবস্থায় শূন্যকে ‘খালি জায়গা’ হিসেবে ব্যবহার করা হতো। সংখ্যার মাঝে এই খালি জায়গা রাখার বিষয়টি থেকে প্রথম শূন্যের ধারণা পাওয়া যায়। পরবর্তীতে এই গণনা ব্যবস্থা ব্যাবিলনীয়রা গ্রহণ করে। ব্যাবিলনীয়রা সুমেরীয়দের থেকে প্রাপ্ত কিউনিফর্মে লিখতো। শুধুমাত্র খালি জায়গা না রেখে ব্যাবলনীয়রা এবার শূন্যকে একটু ভিন্ন মাত্রা দিলো। তারা শূন্য বোঝাতে ২টি কোণাকৃতির (‘’) চিহ্ন ব্যবহার করলো (৭০০ খ্রিস্টপূর্বাব্দদের দিকে ব্যাবিলনের কোথাও কোথাও ১টি কোণাকৃতির (‘) চিহ্নকেও শূন্য ধরা হতো)। যেমন ২৬১, ২৬১’’ (আমাদের গণনা ব্যবস্থার ২৬১০)। তখনও শূন্য শুধুমাত্র খালি স্থান বোঝাতে ব্যবহৃত হতো, কোনো স্বতন্ত্র সংখ্যা হিসেবে নয়। তারও ৬০০ বছর পর ব্যাবিলন থেকে ১২,০০০ মাইল দূরে মায়া সভ্যতার গণিতবিদরাও ক্যালেন্ডারে শূন্যকে ‘খালি জায়গা’ নির্দেশক হিসেবে স্থান দেয়।

Source: damitr.org

এদিকে সমসাময়িক নীল নদের তীরে গড়ে ওঠা মিশরীয় সভ্যতা তখন অনেক এগিয়ে। জ্যোতির্বিজ্ঞান, চান্দ্রবর্ষ, সৌরবর্ষ ভিত্তিক ক্যালেন্ডার তৈরি করে তারা এগিয়ে যাচ্ছিল উন্নত জ্ঞান-বিজ্ঞান চর্চার দিকে। তাছাড়া নীলনদ তীরের নদী গর্ভে হারিয়ে যাওয়া জমি-জমার হিসাব রাখতে তারাই প্রথম জ্যামিতির প্রবর্তন করে। যদিও তা শুধুমাত্র কাজ চলে এমন প্রাথমিক জ্যামিতি। ধীরে ধীরে তারা ঘনবস্তুর ঘনত্ব পরিমাপ করতে শিখে এবং দেড় হাজার বছর ধরে নির্মাণ করা পিরামিডের ঘনত্ব পরিমাপ করতে শেখে (১)।

পরবর্তীতে গ্রিক পন্ডিত ইউক্লিড কিছু স্বতঃসিদ্ধ নীতি বা মৌলিক নিয়মের উপর ভিত্তি করে গণিতের আরেক শাখা জ্যামিতির ভিত্তিপ্রস্তর স্থাপন করেন, যাকে আমরা ‘ইউক্লিডিয়ান জ্যামিতি’ বলে জানি। এতসব জ্ঞানচর্চার মাঝে বিভিন্ন সমস্যা সমাধানের ক্ষেত্রে কখনো কখনো শূন্য বেচারা সামনে চলে আসতো। কিন্তু মিশরীয়রা সযত্নে তাকে হঠিয়ে দিতো এবং কোনোরকম জোড়াতালি দিয়ে সমস্যার সমাধান করতো। কারণ শূন্য ব্যাটা হলো শয়তানের সহচর, ঈশ্বরের পরিপন্থী, ঈশ্বরকে অস্বীকার করে এই পাপিষ্ঠ। তাই শূন্যকে যে করেই হোক ধামাচাপা দেওয়ার চেষ্টা করতো তারা।

শিল্পীর চোখে নীল নদের তীরে প্রাচীন মিশর; Source: aryandawn.com

সেকালের গ্রিক পণ্ডিতেরা জ্ঞানার্জনের জন্য মিশরে যেতেন। মিশরীয়রা তো শূন্যকে অস্বীকার করতো অনেকটা দেখেও না দেখার ভান করার মতো, কিন্তু কখনও অত্যাচার করতো না। কিন্তু গ্রিক পন্ডিতেরা শূন্যকে রীতিমতো কাঠগড়ায় দাঁড় করিয়ে ফেলেছিলেন। পরবর্তীতে এই ভীতির দলে অসীমও যোগ দিয়েছিল। কারণ অসীম মানে সীমাহীন, আর ঈশ্বর হলেন অসীম। জাগতিক সবকিছুই সীমার মাঝে বিদ্যমান এটাই ছিল মিশরীয় পন্ডিতদের বদ্ধমূল ধারণা।

গ্রিক পন্ডিত পিথাগোরাস তো শূন্য এবং অমূলদ কথা শুনলেই কঠিন শাস্তি দিতেন তার গোপন সংঘের শিষ্যদের। তার মতে, শূন্য হলো শয়তানের দোসর আর অমূলদ সংখ্যা হলো বিশ্বপ্রকৃতিতে বিশৃঙ্খলা সৃষ্টিকারী। কারণ গণিতবিদ পিথাগোরাস একজন সঙ্গীতজ্ঞও ছিলেন। বলা চলে, গণিতই তাকে সঙ্গীতের দিকে ঠেলে দিয়েছিল। পিথাগোরাসের শূন্যভীতি তো সভ্যতাক্রমিক কিন্তু অমূলদ সংখ্যার প্রতি বিতৃষ্ণার কারণ হলো তিনি খেয়াল করেছেন যে তারের বাদ্যযন্ত্রগুলোতে যখনই মূলদ সংখ্যার অনুপাতে টোকা দেওয়া হয় তখনই সুরেলা আওয়াজ বের হয়। কিন্তু যখনই তা অমূলদ হয়ে যায় তখনই সেখান থেকে বেসুরো আওয়াজ বের হতে থাকে। এ থেকে পিথাগোরাস একটি বড় সিদ্ধান্তে উপনীত হয়েছিলেন যে, বিশ্ব সংসারে সব কিছুতেই রয়েছে মূলদ সংখ্যারা, অমূলদ সংখ্যা মানেই বেসুর, বিশৃঙ্খলা। আর তাই স্রষ্টা অমূলদ সংখ্যা পছন্দ করেন না এটাই ছিল মহামতী পিথাগোরাসের বদ্ধমূল ধারণা।

পিথাগোরাস আয়ার (Iyer) নামক একটি বাদ্যযন্ত্রের ছবি আঁকছেন; Source: a fresco by Raphael Sanzio

কিন্তু হিপসাস নামক এক হতভাগা শিষ্য সর্বপ্রথম অমূলদ সংখ্যার অস্তিত্ব টের পেয়েছিলেন (২ এর বর্গমূল যে একটি অমূলদ সংখ্যা তা হিপসাসই আবিষ্কার করেছিলেন) এবং তা প্রকাশ করার অপরাধে তাকে পানিতে ডুবে স্বেচ্ছা মৃত্যুদন্ড ভোগ করতে হয়েছিল (২)। কিন্তু সত্য একদিন বেরিয়ে আসবেই। পিথাগোরাস নিজেই অমূলদ সংখ্যার খুব সুন্দর একটি অস্তিত্ব খুঁজে পেয়েছিলেন। গোল্ডেন রেশিও বা সোনালী অনুপাত হলো সেই সৌন্দর্যময় সংখ্যা, প্রকৃতিতে যার হাজারো উদাহরণ রয়েছে। কিন্তু তখনকার দিনে তিনি ছিলেন রীতিমতো দেবতুল্য। একবার যখন ঘোষণা দিয়েই ফেলেছেন যে, শূন্য এবং অমূলদ সংখ্যা ঈশ্বরের পরিপন্থী, সে কথা আবার কোন মুখে তিনি ফিরিয়ে নিবেন। তাই এদের অস্তিত্ব প্রমাণ পেয়েও খুব সযত্নে গোপন রেখেছিলেন পিথাগোরাস ও তার গুপ্ত সংঘের সদস্যরা অর্থাৎ তার অনুসারীরা। এই ছিল গ্রিক সভ্যতায় শূন্যের অবস্থান। এবার মনোযোগ দেওয়া যাক একটু পূর্বে।

ভারতীয় উপমহাদেশে পশ্চিমের নিগৃহীত শূন্য ও অসীম বেশ যত্নে ও মায়ায় বড় হচ্ছিল তখন। কারণ ভারতীয়দের কাছে শূন্য মা ব্রহ্মার প্রতীক (৩)। শূন্য ও অসীম ব্রহ্মারই দুই রুপ। ৪৫৮ খ্রিস্টাব্দে হিন্দুধর্মের পবিত্র গ্রন্থ ঋগ্বেদে প্রথম শূন্যের অস্তিত্ব লক্ষ্য করা যায়। সংস্কৃতে একে ‘শূনিয়া’ বা খালি হিসেবে আখ্যায়িত করা হয়েছিল। তাছাড়া বৌদ্ধ ধর্মেও মনকে খালি করে অর্থাৎ জাগতিক সব চিন্তা ঝেড়ে ফেলে ধ্যানে মনোনিবেশ করার কথা পাওয়া যায়। ভারতের গোয়ালিয়রের এক মন্দিরের শিলালিপিতেও শূন্যের অস্তিত্ব পাওয়া যায়। তাছাড়া খ্রিস্টীয় তিন থেকে চার শতকের মাঝে লেখা বাকশালি পান্ডুলিপিতেও শূন্যের অস্তিত্ব লক্ষ্য করা যায়।  বুঝতেই পারছেন এখানে শূন্যের কতটা কদর ছিল।

বাকশলি পান্ডুলিপিতে শূন্য; Source: ancientpages.com

এদিকে খ্রিস্টীয় চতুর্থ শতকে দিগ্বিজয়ী গ্রিক বীর আলেক্সান্ডার যখন ভারত আক্রমণ করলেন তখন তার সৈন্যসামন্তের মাধ্যমে ভারতীয়রা ব্যবিলনীয়দের গণনা শাস্ত্রের কথা জানতে পারে। ব্যবিলনীয়রা যে শূন্যকে সংখ্যা হিসেবে গ্রহণ না করলেও সংখ্যাব্যবস্থায় ‘স্থানরক্ষক’ হিসেবে গ্রহণ করেছে তা এদের কাছ থেকেই জানতে পারে। এবার ভারতীয়রা আর শূন্যকে নিগৃহীত হতে দিলেন না। শূন্যকে তারা তাদের ১০ ভিত্তিক সংখ্যা মালায় স্থান দিলেন। আনুমানিক ৬২৮ খ্রিস্টাব্দে ব্রহ্মগুপ্ত নামক এক গণিতবিদ সর্বপ্রথম শূন্যকে সংখ্যা হিসেবে ব্যবহার করেন। তিনি শূন্য হিসেবে সংখ্যার নিচে ডট চিহ্ন ব্যবহার করতেন।

গণিতবিদ ব্রহ্মগুপ্ত প্রথম শূন্যকে সংখ্যা হিসেবে ব্যবহার করেন; Source: currentriggers.com

শূন্য দিয়ে যোগ-বিয়োগ-গুণও করেছিলেন তিনি। শূন্য দিয়ে কোনো সংখ্যাকে যোগ বিয়োগ করলে সেই সংখ্যাই পাওয়া যায়। শূন্য দিয়ে গুণ করলে শূন্যই পাওয়া যায় এটাও তিনি জানতেন। কিন্তু বিপত্তি বেঁধেছিল কোনো সংখ্যাকে শূন্য দিয়ে ভাগ করার ক্ষেত্রে। এ ক্ষেত্রে তিনি ভুল একটি করেন তা হলো শূন্য দিয়ে কোনো কিছুকে ভাগ করলে (৪/০) শূন্যই পাওয়া যায়। ১২শ শতাব্দীতে আরেক ভারতীয় গণিতবিদ দ্বিতীয় ভাস্কর প্রমাণ করেন যে, শূন্য দিয়ে ভাগ করলে ফলাফল শূন্য হয় না, হয় অসীম।

অনেকে মনে করেন, ভারতীয়দের মধ্যে প্রথম শূন্যকে সংখ্যার মর্যাদা দেন সেকালের সেরা জ্যোতির্বিজ্ঞানী এবং গণিতবিদ আর্যভট্ট। আর্যভট্ট মাত্র ২৩ বছর বয়সে তার সেরা গ্রন্থ ‘আর্যভটিয়া’ রচনা করেন। বইটির অধিকাংশ লেখাই ছিল গ্রহ নক্ষত্র নিয়ে। চন্দ্রগ্রহণ, সূর্যগ্রহণের সঠিক কারণ, পৃথিবী যে তার অক্ষের উপর দিনে একবার ভ্রমণ করে তা আমরা আর্যভটিয়া থেকেই জানতে পারি। শুধু তা-ই নয়, তিনি ত্রিভুজের ক্ষেত্রফল, পিরামিডের আয়তনও বের করেছিলেন এবং প্রকাশ করেছিলেন এই গ্রন্থে (৩)। কিন্তু এর সবই ছিল বর্ণনামূলক, কোনো গাণিতিক ভাষা তিনি ব্যবহার করেননি। হয়তো তিনি শূন্যকে নিজের অজান্তেই ব্যবহার করেছিলেন, কিন্তু কখনও গাণিতিক ভাষা কিংবা সংখ্যা হিসেবে নয়। তাই আর্যভট্টকে প্রথম শূন্যকে সংখ্যা হিসেবে ব্যবহারকারী বলা যায় না। প্রকৃতপক্ষে শূন্য কেউ কখনো আবিষ্কার করেনি। এমন নয় যে, হঠাৎ কারো মাথায় শূন্য বলে কিছুর উদ্ভব হলো। বরং ধীরে ধীরে প্রস্ফুটিত হওয়া ফুলের মতোই এটি আমাদের সংখ্যামালায় স্থান করে নিয়েছে।

ভারতীয় জ্যোতির্বিদ ও গণিতবিদ আর্যভট্ট; Source: livemint.com

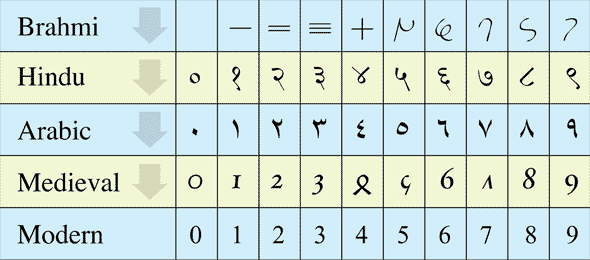
এভাবে ০ ভারতীয়দের ১০ ভিত্তিক সংখ্যামালায় স্থান পায়। ১, ২, ৩…, ৯, ০ যাকে আমরা আরবি নিউমেরাল বলে জানি। কিন্তু আধুনিক ইতিহাসবিদ্গণ একে ভারতীয়দের কৃতিত্ব বলেই মানেন। কারণ আরবরা ভারতীদের কাছ থেকে শেখে, আর পশ্চিমারা আরবদের থেকে। ৭৭৩ খ্রিস্টাব্দে শূন্য ভারত থেকে বাগদাদে এসে উপস্থিত হলো, আরবরাও তাকে সাদরে তাদের সংখ্যামালায় স্থান দিলো। পারস্য মুসলিম গণিতবিদ মুসা আল খোয়ারিজমি শূন্য বোঝাতে গোল বৃত্ত ব্যবহার করলেন, যাকে আজ আমরা শূন্য (০) বলে চিনি। তারপর এর নাম দিলেন ‘সিফর’।

Source: hyd-masti.com

লিওনার্দো ফিবোনাচি নামক এক ইতালীয় শিক্ষার্থী আফ্রিকায় যান উচ্চশিক্ষা লাভের জন্য। এখন যেমন আমাদের দেশের কিংবা প্রাচ্যের শিক্ষার্থীরা পশ্চিমে যায় উচ্চশিক্ষা লাভ করতে, খ্রিস্টীয় দ্বাদশ এবং ত্রয়োদশ শতাব্দীতে ঘটনা ছিল উল্টো। বরং পশ্চিমের মেধাবী শিক্ষার্থীরা আরব, মিশর, ইরাক, সিরিয়ায় যেত উচ্চশিক্ষা লাভের জন্য। তরুণ ফিবোনাচি মুসলিম গণিতজ্ঞদের কাছ থেকে গণিত শিক্ষা লাভ করে দেশে ফিরে যান। কালক্রমে তিনি নিজেও একজন গণিতবিদ হয়ে উঠেন। তিনিই প্রথম আরবি গণিত এবং শূন্যকে ইউরোপীয়দের সামনে তুলে ধরেন। এভাবে ভারতের ‘শূনিয়া’ আরবের ‘সিফর’ হয়ে ধীরে ধীরে পশ্চিমে ‘জিরো’তে পরিণত হলো।

ফিচার ইমেজ- ancient-origins.net

তথ্যসূত্র:

১। শূন্য থেকে মহাবিশ্ব – মীজান রহমান ও অভিজিৎ রায়; শুদ্ধস্বর; প্রথম সংস্করণ; পৃষ্ঠা নং ২০

২। পৃষ্ঠা নং ২২

৩। পৃষ্ঠা নং ৩২

৪। পৃষ্ঠা নং ৩৮