বিজ্ঞানীরা দূরবর্তী গ্রহ-নক্ষত্রের দূরত্ব নির্ণয় করেন কীভাবে?

পত্র পত্রিকায় খবর আসছে, প্রতিনিয়ত গ্রহ, নক্ষত্র, গ্যালাক্সি প্রভৃতি আবিষ্কৃত হচ্ছে। কোটি কোটি কিলোমিটার কিংবা শত শত আলোক বর্ষ দূরে এসব মহাকাশীয় বস্তুর অবস্থান। কিন্তু প্রশ্ন হলো, এরা যে এত দূরে অবস্থান করে তা কীভাবে নির্ণয় করেন বিজ্ঞানীরা? বেশ নিশ্চিত হয়ে বিজ্ঞানীরা কীভাবে বলেন “এত আলোক বর্ষ দূরে অবস্থান করছে অমুক গ্যালাক্সিটি”?

দূরের গ্রহ নক্ষত্রের দূরত্ব বোঝাতে বেশিরভাগ ক্ষেত্রে ‘আলোক বর্ষ’ শব্দটি ব্যবহার করা হয়। সৌরজগতের বাইরে মহাকাশের বস্তুগুলোর দূরত্ব মাপতে সাধারণ কিলোমিটার একক ব্যবহার করা সুবিধাজনক নয়। এত বিশাল দূরত্ব পরিমাপ করতে ‘আলোক বর্ষ’ নামক বিশেষ এই এককটি ব্যবহার করা হয়। আলোক বর্ষের (Light year) বিশালত্ব মানুষের কল্পনাকেও ছাড়িয়ে যায়। আলোর বেগ প্রতি সেকেন্ডে তিন লক্ষ কিলোমিটার। আলো যদি এই বেগে টানা এক বছর ভ্রমণ করে, তাহলে যে দূরত্ব অতিক্রম করবে, তাকে বলে এক আলোক বর্ষ। কিলোমিটারের মাধ্যমে আলোক বর্ষকে প্রকাশ করলে দাঁড়াবে, এক আলোক বর্ষ সমান ৯ মিলিয়ন মিলিয়ন কিলোমিটার (৯×১০^১২ কিলোমিটার)। আমাদের সৌরজগতের সবচেয়ে কাছের নক্ষত্র প্রক্সিমা সেন্টারির দূরত্ব ৪.২ আলোক বর্ষ। দূরের গ্যালাক্সিগুলো শত শত কিংবা হাজার হাজার আলোক বর্ষ পর্যন্ত দূরে অবস্থান করে। এত বিশাল দূরত্ব মাপার কৌশলটা কী?

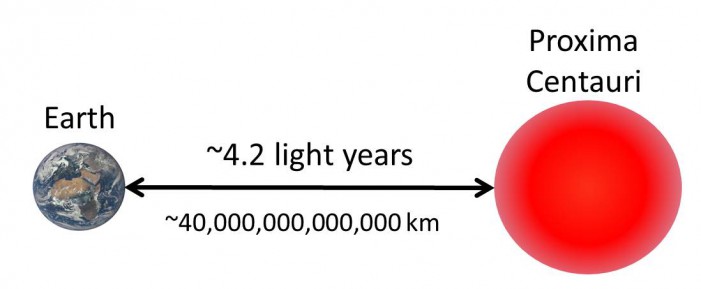
সৌরজগতের সবচেয়ে কাছের নক্ষত্রের দূরত্বও ৪ আলোকবর্ষের চেয়ে বেশি। ছবি: ন্যাশনাল স্কুল অবজারভেটরি ইউকে

অকল্পনীয় দূরে অবস্থান করলেও আমাদের পক্ষে এদের দূরত্ব পরিমাপ করা সম্ভব। গ্যালাক্সিগুলোতে অবস্থান না করেও চমৎকার কিছু কৌশল ব্যবহার করে তাদের দূরত্ব বের করে ফেলা যায়। তুলনামূলকভাবে নিকটবর্তী নক্ষত্রগুলোর দূরত্ব পরিমাপে ‘প্যারালাক্স’ পদ্ধতি ব্যবহার করা হয়। শব্দটি শুনতে অন্যরকম মনে হলেও, এটি আসলে একদমই সহজ একটি ট্রিক। এই ট্রিকটি হাতে কলমে এখনই আমরা শিখে ফেলতে পারি।

প্রথমে মুখের সামনে হাতের একটি আঙুল তুলে ধরতে হবে। এরপর বাম চোখ বন্ধ করে শুধুমাত্র ডান চোখ দিয়ে আঙুলটির দিকে তাকাতে হবে। এরপর আবার ডান চোখ বন্ধ রেখে বাম চোখ দিয়ে আঙুলের দিকে তাকাতে হবে। একবার ডান চোখ আরেকবার বাম চোখ, এভাবে কয়েকবার করলে মনে হবে আঙুলটির অবস্থান এদিক ওদিক হচ্ছে। আদতে আঙুলটি কিন্তু একই স্থানে আছে, দুই চোখের ভিন্ন ভিন্ন অবস্থানের কারণে আঙুলটিও ভিন্ন ভিন্ন অবস্থানে আছে বলে মনে হয়।

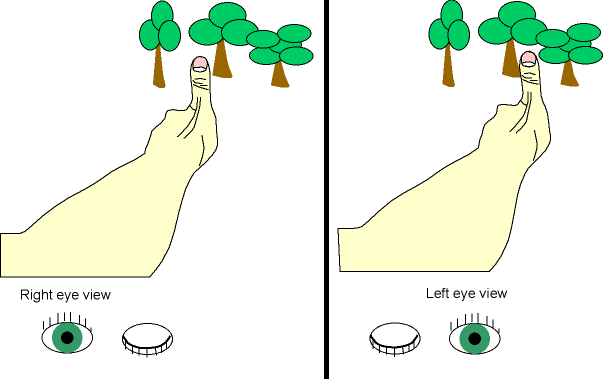
বুড়ো আঙুলের সাহায্যে প্যারালাক্স। ছবি: এস্ট্রোনমি নোটস

আঙুলকে চোখের আরো কাছে নিয়ে আসলে আঙুলের নড়াচড়া আরো বেড়ে যাবে। কাছে না এনে যদি আঙুলকে দূরে নেয়া হয় তাহলে নড়াচড়া অল্প স্থানের মধ্যে সীমাবদ্ধ হয়ে যাবে। এখান থেকে আমরা বুঝতে পারছি, দুই চোখের দুই ভিন্ন অবস্থানের সাপেক্ষে আঙুলের অবস্থান পাল্টে যাবার পরিমাণ বেশি হলে, সেটি নিকটে অবস্থিত আর অবস্থান পরিবর্তনের পরিমাণ কম হলে, সেটি দূরে অবস্থিত। যদি কোনোভাবে আমরা দুই চোখের পারস্পরিক দূরত্ব ও লক্ষ্যবস্তুর বিচ্যুত হবার পরিমাণ বের করতে পারি, তাহলে ত্রিকোণমিতির সূত্র প্রয়োগ করে বের করতে পারবো লক্ষ্যবস্তুর দূরত্ব কত। নক্ষত্রদের বেলাতেও একই পদ্ধতি ব্যবহার করে তাদের দূরত্ব পরিমাপ করা সম্ভব।

এই পদ্ধতিতে নক্ষত্রের দূরত্ব পরিমাপ করার জন্য আঙুলের বদলে নক্ষত্রকে লক্ষ্য করে ডান চোখ ও বাম চোখ দিয়ে তাকালে দেখা যাবে, কোনো পরিবর্তন হচ্ছে না। কারণ নক্ষত্র এতই বেশি দূরে অবস্থান করে যে, দুই চোখের কাছাকাছি অবস্থান তেমন কোনো কৌণিক বিচ্যুতি তৈরি করতে পারে না। দুই চোখ যদি পরস্পর থেকে কয়েক মিলিয়ন কিলোমিটার দূরে অবস্থান করতো, তাহলে এদের দ্বারা প্যারালাক্স পদ্ধতিতে নক্ষত্রদের দূরত্ব পরিমাপ করা যেত।

খালি চোখে নক্ষত্রের প্যারালাক্স পর্যবেক্ষণ করতে হলে দুই চোখকে পরস্পর থেকে মিলিয়ন মিলিয়ন কিলোমিটার দূরে অবস্থান করতে হবে। ছবি: মাই কিউট গ্রাফিক্স

চোখকে হয়তো মিলিয়ন মিলিয়ন কিলোমিটার দূরে অবস্থান করানো সম্ভব না, কিন্তু বিজ্ঞানীরা এর বিকল্প পদ্ধতি খুঁজে নিয়েছেন। আসলে কোনো কিছুকে বৈজ্ঞানিক দৃষ্টিকোণ থেকে বিচার বিশ্লেষণ করলে, তার মধ্যে হাজার রকমের সমস্যা দেখা দেয় এবং এসব সমস্যার বিপরীতে হাজার রকমের চমকপ্রদ সমাধানও এসে ধরা দেয়। বিজ্ঞানীরা মহাকাশীয় বস্তুর দূরত্ব মাপতে পৃথিবীর কক্ষপথীয় ঘূর্ণনকে ব্যবহার করেন। সূর্যের চারপাশে পৃথিবীর কক্ষপথের ব্যাস ১৮৬ মিলিয়ন মাইল। আজকে পৃথিবী কক্ষপথের যে অবস্থানে আছে এবং ঠিক ছয় মাস পরে যে অবস্থানে থাকবে তাদের পারস্পরিক দূরত্ব হবে ১৮৬ মাইল। এটি মোটামুটি যথেষ্ট লম্বা দূরত্ব। এত পরিমাণ দূরত্বে দূরবর্তী নক্ষত্রের প্যারালাক্স অনায়াসেই শনাক্ত করা যাবে।

কক্ষপথের কোনো অবস্থান থেকে নক্ষত্রের অবস্থানের মাপ নিয়ে, ছয় মাস পর আবারো ঐ নক্ষত্রের মাপ নিলে প্যারালাক্স পদ্ধতির মাধ্যমে তার দূরত্ব নির্ণয় করা যাবে। এখানে যেহেতু ছয় মাস আগে ও ছয় মাস পরে পৃথিবীর দুই অবস্থানের দূরত্ব জানা আছে এবং নক্ষত্রের অবস্থান চ্যুতি জানা আছে, তাই ত্রিকোণমিতির সূত্রের মাধ্যমে এখান থেকে নক্ষত্রের দূরত্ব বের করা খুব কঠিন কিছু নয়।

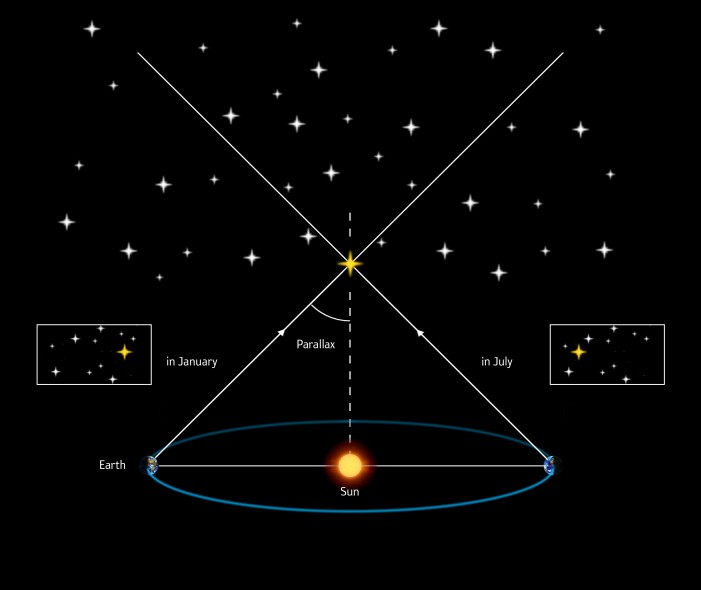
বড় পড়িসরে প্যারালাক্স। ছবি: ইএসএ ইন্টারন্যাশনাল

কিন্তু এত বিশাল দূরত্বকে ব্যবহার করার পরেও সকল নক্ষত্রের দূরত্ব এর মাধ্যমে বের করা যায় না। এই পদ্ধতিতে শুধুমাত্র নিকট দূরের নক্ষত্রগুলোর দূরত্ব পরিমাপ করা যায়। অতীব দূরের নক্ষত্রগুলোর বেলায় এই পদ্ধতিতে দূরত্ব বের করা যায় না। এরা এতটাই দূরে যে, ১৮৬ মিলিয়ন মাইলের প্যারালাক্স দুূরত্বও এখানে কিছু না।

এদের দূরত্ব পরিমাপ করতে হলে প্যারালাক্স পদ্ধতির বিকল্প কিছু একটা ভাবতে হবে। এর বিকল্প হতে পারে উজ্জ্বলতা। কোনো নক্ষত্র বা কোনো গ্যালাক্সি কতটুকু উজ্জ্বল তার মাধ্যমে দূরত্ব বের করা যেতে পারে। কোনো নক্ষত্র যদি কাছে থাকে তাহলে তাকে অধিক উজ্জ্বল দেখাবে আর কোনো নক্ষত্র যদি দূরে থাকে তাহলে তাকে কিছুটা অনুজ্জ্বল দেখাবে।

উজ্জ্বলতা বিবেচনা করে দূরত্ব পরিমাপ করার ব্যাপারটি আপাতভাবে সুন্দর হলেও, এতে বেশ কিছু ঝামেলা আছে। সব নক্ষত্রের উজ্জ্বলতা সমান নয়। নক্ষত্রের আকার ও ভরের উপর তার উজ্জ্বলতা নির্ভর করে। অনুজ্জ্বল নক্ষত্রটি যদি কাছে থাকে আর উজ্জ্বল নক্ষত্রটি যদি দূরে থাকে, তখন এই ব্যাপারটির মীমাংসা কীভাবে করা হবে? মৃদু উজ্জ্বল মোমবাতি যদি কাছে থাকে আর অধিক উজ্জ্বল মোমবাতি যদি দূরে থাকে, তাহলে আপেক্ষিকভাবে তাদের উজ্জ্বলতা সমান বলে মনে হতে পারে। কিংবা এমনও হতে পারে, অবস্থানের কারণে হালকা উজ্জ্বলতার মোমবাতিটিকেই বেশি উজ্জ্বল বলে প্রতিভাত হচ্ছে। নক্ষত্রদের বেলাতেও এরকম ব্যাপার প্রযোজ্য। তাই উজ্জ্বলতা দিয়ে দূরত্ব পরিমাপ করতে গেলে তা সমস্যার সৃষ্টি করবে।

সৌভাগ্যক্রমে, বিজ্ঞানীরা বিশেষ ধরনের একটি পদ্ধতি ব্যবহার করে দূরবর্তী নক্ষত্রের দূরত্ব পরিমাপ করতে পারেন। তারা বিশেষ কিছু নক্ষত্রকে ‘প্রমাণ নক্ষত্র’ হিসেবে ধরে নেন এবং এদের সাপেক্ষে অন্য নক্ষত্রের দূরত্ব পরিমাপ করতে পারেন। এসব নক্ষত্রের উজ্জ্বলতা ও তীব্রতা নির্দিষ্ট থাকে। বিজ্ঞানীরা এও জানেন, কীভাবে এরকম প্রমাণ নক্ষত্র (Variable Star) খুঁজে বের করতে হবে। এরকম নক্ষত্রের সাহায্যে, প্রতিষ্ঠিত কিছু গাণিতিক সূত্রাবলি প্রয়োগ করে বের করা যায় দূরবর্তী নক্ষত্রগুলো কত দূরে অবস্থিত।

ট্রিফিড নীহারিকায় কয়েকটি প্রমাণ নক্ষত্র। ছবি: উইকিমিডিয়া কমন্স/ESO/D. Minniti

গ্যালাক্সি বা নক্ষত্র যত দূরেই থাকুক, কোনো না কোনো ভাবে আমরা তাদের অবস্থান ও দূরত্ব বের করতে পারি। নিকটবর্তী নক্ষত্রের জন্য আমাদের আছে প্যারালাক্স পদ্ধতি আর দূরবর্তী নক্ষত্রের জন্য আমাদের আছে ‘প্রমাণ নক্ষত্র’ পদ্ধতি।

বিজ্ঞান এই একটা দিক থেকে অনন্য। কোনো একটা ব্যাপার যতই ধরাছোঁয়ার বাইরে হোক না কেন, বিজ্ঞানকে ব্যবহার করে মানুষ কিছু একটা উপায় ঠিকই খুঁজে নেয়। বিজ্ঞানের মারপ্যাঁচে সমস্যার সমাধান বের হয়ে যায় ঠিকই।

ফিচার ছবি: Pic2.me