গণিতের যোগ, বিয়োগ, গুন ও ভাগ চিহ্ন এলো কীভাবে?

গণিত হচ্ছে বিশ্বের ভাষা। তাই আপনি যত বেশি সমীকরণ জানবেন, তত বেশি মহাজগতের সাথে যোগাযোগ করতে পারবেন।- নিল ডিগ্রেস টাইসন

শুধু মার্কিন এই জ্যোতিঃপদার্থবিজ্ঞানী নন, পৃথিবীর অনেক বিজ্ঞানীই গণিত নিয়ে করে গেছেন এমন অনেক উক্তি। না করেই বা উপায় কী? আসলেই তো আমরা সবাই প্রাত্যহিক জীবনে গণিত ছাড়া অচল। এই যেমন, সকালে কখন ঘুম থেকে উঠবেন, সেটাও ঠিক করেন সংখ্যা দিয়ে। ঘুম থেকে উঠে প্রথমে কী কাজ করবেন, দ্বিতীয় কাজ কী হবে; এই ‘প্রথম’, ‘দ্বিতীয়’ও গণিতের অংশ। এই গণিতের ইতিহাস সুবিশাল। তবে আজকের গল্পটা গণিতকে নিয়ে না, গণিতের একটি অংশ নিয়ে; ‘গাণিতিক চিহ্ন’ নামেই তার পরিচয়।

গণিতের এ অংশের সদস্য সংখ্যা মোটেও কম না। যোগ, বিয়োগ, গুন, ভাগ, সমান, বর্গমূল, পাই, বন্ধনী, সমানুপাতিক, ব্যস্তানুপাতিক আরও কত কী! চিহ্নের প্রচলনের অনেক আগেও সে চিহ্নের যে কাজ, তার প্রচলন ছিল। কিন্তু সেক্ষেত্রে পুরো প্রক্রিয়াটি কথায় লিখে প্রকাশ করতে সময় ও শ্রম দুটিই বেশি প্রয়োজন হতো। তাই সময় অপচয় রোধের উদ্দেশ্যেই চিহ্নের ব্যবহার শুরু। উদাহরণস্বরূপ বলা যেতে পারে, ২ ও ৩ এর যোগ করতে আমরা কত সহজেই লিখে ফেলি ‘২ + ৩’। কিন্তু যখন এই যোগ চিহ্নের উৎপত্তি হয়নি, তখন লিখতে হতো, ‘২ এর সাথে ৩ যোগ করো’।

আবার ‘২ + ৩’ এর ফলাফল ৫, যা আমরা সহজেই প্রকাশ করতে পারি ২ + ৩ = ৫ লিখে। কিন্তু যখন পর্যন্ত ‘সমান’ চিহ্নের উৎপত্তি হয়নি, তখন এর পরিবর্তে লিখতে হতো ‘ইজ ইকুয়ালস টু’, যা অপেক্ষাকৃত সময়সাপেক্ষ ব্যাপার ছিল। তাই ওয়েলসের গণিতজ্ঞ রবার্ট রেকর্ড তার বই ‘দ্য ওয়েটস্টোন অব উইট’ লিখতে গিয়ে প্রচলন ঘটালের সমান (=) চিহ্নের। এবার তবে আলাদা আলাদা করে চিহ্নদের গল্প করা যাক।

যোগ

দুই বা ততোধিক সংখ্যাকে একসাথে গণনা করতে যে চিহ্ন ব্যবহৃত হয়ে থাকে, তা-ই যোগ চিহ্ন। আরও বাড়ানোর নিমিত্তেই যোগ করার প্রক্রিয়া। যোগ শব্দের আগমন ল্যাটিন শব্দ Plus থেকে, যার অর্থ ‘আরও’। ল্যাটিন ‘Et’ থেকে & (And)-এর আগমন। এই ‘and’ এর পরিবর্তেই ‘+’ চিহ্ন ব্যবহার করা শুরু হয়। যতদূর জানা যায়, যোগ চিহ্ন হিসেবে ‘+’ এর ব্যবহার শুরু হয় চতুর্দশ শতাব্দীতে। নিকোলাস ওরেসমে তার ‘অ্যালগোরিসমাস প্রোপোর্শনাম’-এ প্রথমবার ‘+’ চিহ্ন ব্যবহার করেন বলে জানা যায়। তবে সে সময়েই এটি বিশ্বব্যাপী সমাদৃত হয়েছে, এমনটা নয়। অনেকেই আরও অন্য অনেক ধরনের প্রতীক ব্যবহার করতেন। যেমন, ইতালিয় গণিতবিদ ‘লুকা প্যাসিওলি’ যোগ বোঝাতে ব্যবহার করতেন ইংরেজি ‘p’ এর উপর একটি ছোট দাগ দিয়ে। ‘+’ চিহ্নের প্রচলন ব্যপকভাবে ঘটে জোহানেস উইডম্যান নামক জার্মান গণিতবিদ তার ‘মার্সেন্টাইল অ্যারিথমেটিক’ বইয়ে এ চিহ্ন ব্যবহার করলে।

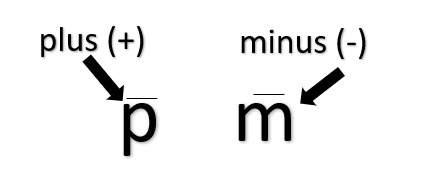
বিয়োগ

বাদ দেওয়াকেই বিয়োগ বোঝায়। ‘বিয়োগ’ শব্দের উৎপত্তি ল্যাটিন শব্দ ‘minus’ থেকে, যার অর্থ ‘less’ বা কম। লুকাস প্যাসিওলি যোগের মতো বিয়োগের ক্ষেত্রে শুধু ‘p’-এর স্থলে ‘m’ ব্যবহার করতেন। তবে বিয়োগ চিহ্ন হিসেবে ‘–‘ এর ব্যবহার ঠিক কবে থেকে শুরু হয়েছে, তা স্পষ্ট জানা যায় না। খুব সম্ভবত চতুর্দশ শতাব্দীতেই যোগের সাথে বিয়োগেরও উৎপত্তি। বিয়োগ ব্যপকভাবে ব্যবহৃত হতে শুরু করে ‘মার্সেন্টাইল অ্যারিথমেটিক’ বইয়ে এর ব্যবহারের পরেই। উল্লেখ্য, ইংরেজদের কাছে যোগ এবং বিয়োগ চিহ্ন প্রথম তুলে ধরেন রবার্ট রেকর্ড’ তার বই ‘দ্য ওয়েটস্টোন অব উইট’-এ ব্যবহারের মাধ্যমে।

গুন

(×) কিংবা (.); বর্তমান সময়ে গুন বোঝাতে এই দুটি চিহ্নই বহুল ব্যবহৃত। যদিও দ্বিতীয়টির ডট প্রোডাক্ট হিসেবে আলাদা ব্যবহার আছে, তবে প্রথমটিই অধিক ব্যবহৃত হয় সাধারণ গুন বুঝাতে। এ চিহ্নের ব্যবহার শুরু হয় ষোড়শ শতাব্দীতে। বলা হয়ে থাকে, ইংরেজ গণিতবিদ উইলিয়াম অটরেড সর্বপ্রথম এ চিহ্নের ব্যবহার করেন। তবে ঠিক কী কারণে এটির মাধ্যমেই গুন প্রক্রিয়াকে চিহ্নায়িত করা হয়, তা নিশ্চিত নয়। বলা হয়ে থাকে, তিনি সেন্ট এন্ড্রু ক্রস থেকে এর ব্যবহার করেন।

আবার অনেকেরই ধারণা, যেহেতু গুন মূলত অনেক বড় যোগ প্রক্রিয়াকেই সহজতর করেছে, তাই যোগ চিহ্নকেই আড়াআড়িভাবে ব্যবহার করে গুন চিহ্নের ব্যবহার শুরু করা হয়েছে। তবে এটি ইংরেজি ‘x’-এর সাথে মিলে যাওয়ায় জার্মান দার্শনিক ও গণিতবিদ গটফ্রিড এ চিহ্নকে প্রত্যাখ্যান করে শুধু একটি ডট ব্যবহার করেন, যা এখনো অনেকটাই প্রচলিত।

ভাগ

ভাগ চিহ্ন হিসেবে আমরা অনেক চিহ্নের ব্যবহারই দেখে থাকি এই একবিংশ শতাব্দীতেও। এদের মধ্যে সবথেকে বেশি ব্যবহৃত হয়ে থাকে ‘÷’, ‘/’, ‘x) y (z’ এবং ‘।’; সবশেষে উল্লেখ করা ধরনটির ব্যবহারই হয়তো সবার আগে শুরু হয়েছে, আনুমানিক ত্রয়োদশ শতাব্দীরও আগে। তবে ব্যবহারে ব্যাপকতা লাভ করে ষোড়শ শতাব্দীতে এসে। এটি সামনে আনে আরবীয়রা, এবং পরবর্তী সময়ে ইয়োরোপীয় গণিতবিদ ফিবোনাচ্চি এটি ব্যবহার করেন ষোড়শ শতাব্দী। ‘/’ চিহ্ন দিয়ে ভাগ বোঝানো শুরু হয় ১৮৪৫ সালে ডি মরগানের হাত ধরে।

তবে বহুল প্রচলিত ভাগ চিহ্ন (÷)-এর ব্যবহার প্রথমবার করেন সুইস গণিতবিদ জোহান রাহন, ১৬৫৯ সালে তার Teutsche Algebra নামক বইতে। যদিও এই চিহ্নটির আন্তর্জাতিক স্বীকৃতি নেই বর্তমানে। ভাগ চিহ্ন হিসেবে ‘/’-এর ব্যবহারই বর্তমান সময়ে আদর্শ হিসেবে স্বীকৃত।

সমান

১৫৫৭ সালে ওয়েলসের গণিতবিদ রবার্ট রেকর্ড তার বই ‘দ্য ওয়েটস্টোন অব উইট’ লিখেছিলেন তার ইংরেজ ছাত্রদের জন্য। সে বইয়ে উনি বারবার ‘is equals to’ লিখতে লিখতে বিরক্ত বোধ করার ফলে দু’টি সমান, আনুভূমিক এবং সমান্তরাল দাগ (=) ব্যবহার করেন, যা পরবর্তী সময়ে জনপ্রিয়তা পেয়ে যায় এবং এখনো ব্যবহৃত হয়ে আসছে। কেউ কেউ তখন দু’টি উল্লম্ব সমান ও সমান্তরাল দাগকেও সমান চিহ্ন হিসেবে ব্যবহার করেছেন। তবে ‘=’ চিহ্নটিই অধিক গ্রহণযোগ্যতা পায়।

যোগ, বিয়োগ, গুন, ভাগ এবং সমান চিহ্নের উৎপত্তি নিয়ে আলোচনা করা আপাতত শেষ, তবে গণিতের চিহ্ন আছে আরও অগণিত। সেসবের কয়েকটি নিয়ে খানিক কথা বলে শেষ করা যাক।

ব্রিটিশ জন ওয়ালিস ১৬৫৫ সালে অসীম বা ইনফিনিটি চিহ্ন প্রথম ব্যবহার করেন। ১৭০৬ সালে পাই চিহ্নের (π) চিহ্নের প্রচলন ঘটান উইলিয়াম জোনস। ১৫২৫ সালে রুডলফ সামনে আনেন স্কোয়ার রুট বা বর্গমূল চিহ্নকে। বীজগণিতের প্রথম জার্মান পাঠ্যবই তারই লেখা। sin, cos, tan এর ব্যবহার শুরু করেন ইউলার, সময়কাল ১৭৪৮ থেকে ১৭৫৩। ১৮০৮ সালে ক্র্যাম্প ফ্যাক্টোরিয়াল চিহ্ন হিসেবে ব্যবহার করতে শুরু করেন ‘!’-কে।

এভাবেই শতাব্দীর পর শতাব্দী ধরে অগণিত মানুষের হাত ধরে বিবর্তিত হয়ে আমাদের কাছে এসে পৌঁছেছে এসকল গাণিতিক চিহ্ন। এসব চিহ্ন আমাদের জীবনযাত্রাকে করেছে সহজতর। আর বিশ্বব্যাপী এখনো একই চিহ্নকে আদর্শ হিসেবে ব্যবহার করতে কাজ করে যাচ্ছে আইএসও বা ইন্টারন্যাশনাল অর্গানাইজেশন অভ স্ট্যান্ডার্ডাইজেশন।