গ্রিক পুরাণের বীর অ্যাকিলিস আজ ঢাল-তরবারি ফেলে খেলার ময়দানে যোগ দিয়েছেন। অনেক হলো যুদ্ধ-বিগ্রহ! এবার সবকিছু ছেড়ে শান্তির পথের পথিক হবেন তিনি। নতুন জীবনের শুরুটা স্মরণীয় করতে এক দৌড় প্রতিযোগিতার আয়োজন করা হয়েছে। সুঠাম দেহের অধিকারী অ্যাকিলিসকে দৌড়ে হারানো সহজ হবে না। এজন্য প্রয়োজন শক্ত প্রতিপক্ষ। কিন্তু সবাইকে অবাক করে দিয়ে অ্যাকিলিসের বিরুদ্ধে দৌড় প্রতিযোগিতায় লড়তে হাজির হলো প্রাণীজগতের অন্যতম ধীরগতিসম্পন্ন প্রাণী কচ্ছপ।
সবাই কচ্ছপের সাহস দেখে হাসতে থাকলো। অনেকে ফিসফিস করতে থাকলো, “বোকা খরগোশের সাথে পেরেছো বলে অ্যাকিলিসের সাথে পারবে, এটা কচ্ছপটা ভাবলো কী করে?” কচ্ছপ কারো কথা কানেই তুললো না। সে ভারিক্কি ভঙ্গিতে কোমর বেঁধে নেমে পড়লো ময়দানে। অ্যাকিলিস সহজ প্রতিপক্ষ পেয়ে যেন আরো উৎসাহী হয়ে উঠলেন। তিনি কচ্ছপকে তুচ্ছ মনে করে শুরুর দাগ থেকে আরো কয়েক মিটার পেছনে থেকে দৌড় শুরু করবেন বলে সিদ্ধান্ত নিলেন। বিচারক নিজেও কচ্ছপের প্রতি সামান্য সহানুভূতি প্রকাশ করে এই সিদ্ধান্ত মেনে নিলেন।
কাঙ্ক্ষিত সেই দৌড় প্রতিযোগিতা শুরু হবে আর কিছুক্ষণের মধ্যে। এবার পাঠক আপনারাই বলুন, কে জিতবে এই দৌড়? অ্যাকিলিস নাকি কচ্ছপ? স্বাভাবিকভাবে আমরা বলতে পারি, এই প্রতিযোগিতার বিজয়ী হবে অ্যাকিলিস। কিন্তু কেউ যদি মনে করেন, এই প্রতিযোগিতার বিজয়ী হবে কচ্ছপ, তাহলে তাকে স্বাগতম জানাচ্ছি এক নতুন জগতে, যার নাম ‘জেনোর প্যারাডক্স‘ জগত। এই জগতে অ্যাকিলিস যতই চেষ্টা করুক, তিনি কখনোই কচ্ছপকে হারাতে পারবেন না।
জেনোর প্যারাডক্স কী?
জেনোর প্যারাডক্সের প্রবর্তক গ্রিক দার্শনিক জেনো অফ ইলিয়া। আনুমানিক ৪৯০ খ্রিস্টপূর্বে জন্মগ্রহণ করা এই দার্শনিক দক্ষিণ ইতালিতে ইলিয়াতিক স্কুল নামক একটি বুদ্ধিচর্চা কেন্দ্রে অধ্যয়ন করতেন। জেনোর সাথে আমরা পরিচিত হই মহান দার্শনিক প্লেটোর বিভিন্ন লেখনীর মাধ্যমে। জেনো তার স্কুলে বিভিন্ন শিষ্যদের সাথে নিজের চিন্তাভাবনা নিয়ে আলোচনা করতেন। সেখান থেকে তিনি তার প্যারাডক্সের আজব দুনিয়ার সন্ধান লাভ করেন।
জেনোর প্যারাডক্সগুলো প্রাচীন বিজ্ঞান জগতের সুবিখ্যাত গোলকধাঁধা। আপাতদৃষ্টিতে যা আমাদের নিকট স্বাভাবিক লাগে, সে ধরনের পরিস্থিতিকে বিভিন্ন প্যারাডক্সের ফাঁদে ফেলে জেনো একধরনের নতুন সমস্যার সৃষ্টি করেন। এই প্যারাডক্সের ধাঁধায় আটকে যায় আমাদের স্বাভাবিক চিন্তাধারা। কারণ, যুক্তি-তর্ক দিয়ে জেনোর প্যারাডক্সগুলো প্রমাণ করা বেশ কষ্টসাধ্য ব্যাপার। এমনকি জেনোর দশটি প্যারাডক্সের মাঝে অনেকগুলো প্রায় কয়েক শতাব্দী ধরে অমীমাংসিত ছিল। এই সমস্যাগুলোকে গণিতের জগতের নিদর্শন হিসেবে গণ্য করা হয়, যা প্রায় আড়াই হাজার বছর ধরে টিকে আছে।

এই প্যারাডক্সগুলোর মাঝে সবচেয়ে মজার সমস্যাটি সম্ভবত বীর অ্যাকিলিস এবং কচ্ছপের সেই দৌড় প্রতিযোগিতাকে ঘিরে। আর যেহেতু জেনোর প্যারাডক্সের জগতে অনেক কিছু সম্ভব, তাই সেখানে অ্যাকিলিসের চূড়ান্ত পরাজয় হয়েছিল এক কচ্ছপের কাছে।
অ্যাকিলিস বনাম কচ্ছপ
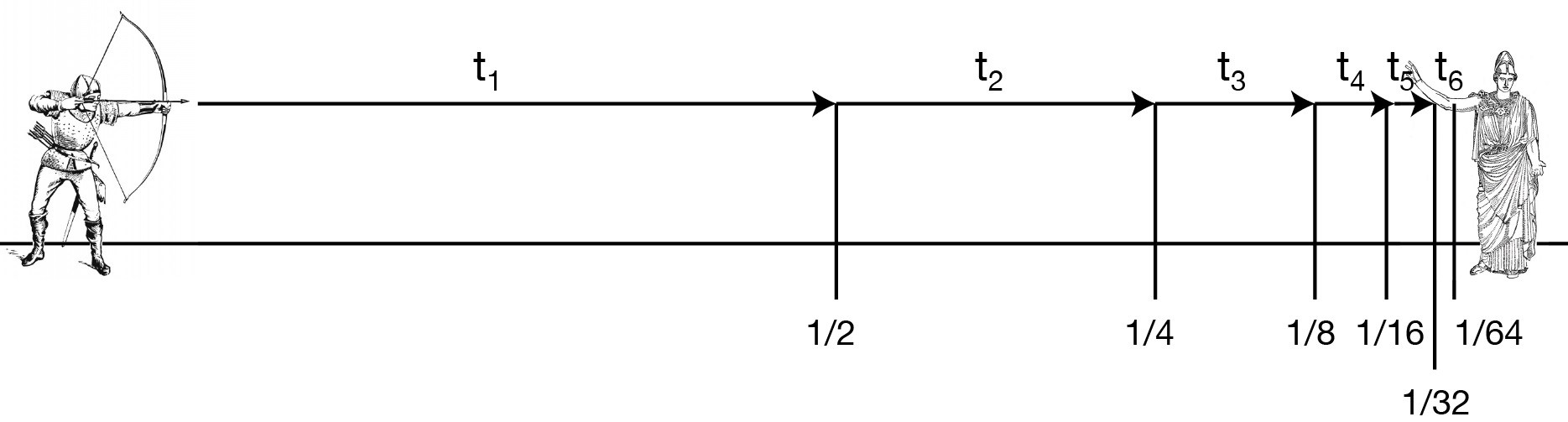
বিচারক আকাশের দিকে বন্দুক তাক করে ফাঁকা গুলি ছুঁড়তেই অ্যাকিলিস দৌড় শুরু করলেন। কচ্ছপও গুটি গুটি পায়ে এগোনো শুরু করলো। ধরি, আকিলিস যখন দৌড় শুরু করলেন, তখন কচ্ছপের অবস্থান ছিল ‘x’। অ্যাকিলিস দৌড়ে ‘x’ অবস্থানে পৌঁছে গেলেন। কিন্তু ততক্ষণে কচ্ছপটি সামান্য এগিয়ে নতুন অবস্থান ‘y’ তে পৌঁছে গেছে। তাই অ্যাকিলিস আবার দৌড়ে ‘y’ পর্যন্ত পৌঁছে গেলেন। কিন্তু ততক্ষণে কচ্ছপটা সামান্য এগিয়ে আরেক নতুন অবস্থান ‘z’-এ পৌঁছে যাবে।
চটে গেলেন অ্যাকিলিস। কিন্তু কিছু করার নেই। তাই তিনি পুনরায় ‘z’ পর্যন্ত দৌড়ে গেলেন। কিন্তু কী বিপদ! কচ্ছপটা যে তখন আরেক নতুন অবস্থানে এগিয়ে গেলো। এভাবে অ্যাকিলিস যতবারই চেষ্টা করছেন কচ্ছপের অবস্থানে পৌঁছে কচ্ছপকে ধরার, ততবারই কচ্ছপটি হাতছাড়া হয়ে যাচ্ছে। যেন পেছন থেকে দৌড় দেয়ার পুরো বুদ্ধিটাই সকল নষ্টের মূল। আর সবাই অবাক হয়ে দেখলো, অ্যাকিলিস কচ্ছপটিকে ধরতেই পারছেন না। তাই অ্যাকিলিস কচ্ছপের পেছনে পড়ে রইলেন।
গণিতের দৃষ্টিতে জেনোর প্যারাডক্স
এবার গণিতের মঞ্চে আমরা অ্যাকিলিসের দৌড়কে পর্যবেক্ষণ করি। ধরি, অ্যাকিলিস কচ্ছপের ১০ মিটার পেছন থেকে দৌড় শুরু করেছিলেন। মনে করি, অ্যাকিলিসের গতিবেগ সেকেণ্ডে ১০ মিটার। কচ্ছপের গতিবেগ সেকেণ্ডে ১ মিটার। এবার ধরা যাক, দৌড় শুরু হবার এক সেকেণ্ড পরে অ্যাকিলিস পৌঁছে গেলেন কচ্ছপের অবস্থানে। আর কচ্ছপ তার গতিবেগ অনুযায়ী চলে গেলো আরো ১ মিটার সামনে। এবার ধরা যাক, অ্যাকিলিস পুনরায় যখন ১ মিটার দৌড়ে গেলেন, তখন কচ্ছপটি পৌঁছে যাবে আরো ০.১ মিটার। আকিলিস যখন পুনরায় ০.১ মিটার অতিক্রম করবেন, তখনো কচ্ছপটি ০.০১ মিটার এগিয়ে থাকবে। ঠিক উপরের প্যারাডক্সের মতো এভাবে কচ্ছপটি সর্বদা সামনে এগিয়ে থাকবে। অ্যাকিলিস দ্বারা অতিক্রান্ত দূরত্বকে জ্যামিতিক সিরিজ আকারে সাজালে আমরা পাই,
দূরত্ব = 10 + 1 + 0.1 + …. + 10 (2-n) + …
পুরো ব্যাপারটি এখনই যেন মাথা ধরিয়ে দিচ্ছে! কারণ, গণিতের হিসাব অনুযায়ী, অ্যাকিলিস মাত্র ১.১১ সেকেণ্ডে কচ্ছপটিকে অতিক্রম করে সামনে এগিয়ে যাওয়ার কথা। তাহলে ঠিক কোন কারণে জেনোর প্যারাডক্সে বারবার পিছিয়ে যাচ্ছেন অ্যাকিলিস? আসল ফাঁকিটা কোথায়?

জেনোর ফাঁকি
জেনো একটি নতুন জগতের কল্পনায় বিভোর ছিলেন। এই অদ্ভুত জেনোর জগতে অবস্থান এবং সময়কে অসীম ভাগে বিভাজিত করা যায়। যেন পুরো দৌড়ের ময়দানকে জেনো তার কল্পনায় কোটি কোটি বার ভাগ করে ফেলেছেন। সেখানে বেচারা অ্যাকিলিস এক প্রাণান্তকর দৌড়ে বার বার পিছিয়ে পড়ছেন মন্থরগতির কচ্ছপ থেকে।
জেনোর এই বিভাজনের কোনো শেষ নেই। এমনকি ময়দানের দূরত্বকে এরূপ অসীম ভাগে বিভাজিত করার ফলে জেনোর প্যারাডক্সে সময়ও ধীর হয়ে পড়েছে। যার ফলে অ্যাকিলিস কখনোই এগিয়ে যেতে পারছেন না। ঠিক এখানেই জেনোর ফাঁকি কাজ করছে। কারণ, আমরা জানি সময়কে এভাবে বিভাজিত করে ধীর করা সম্ভব নয়। তাই জেনোর প্যারাডক্সের শক্তিশালী দুর্গের এই দুর্বলতা পুরো ধাঁধার ভিতকে ভেঙে দিয়েছে।

তাই যদিও অ্যাকিলিসের কচ্ছপকে অতিক্রম করতে হলে একটি নির্দিষ্ট সময় প্রয়োজন ছিল, কিন্তু সময়কে অসীম ভাগে বিভক্ত করার ফলে তিনি কখনোই সেই নির্দিষ্ট সময় পর্যন্ত দৌড়াতে পারবেন না। এই অদ্ভুত ধারণার ফলেই জেনোর প্যারাডক্সে আমাদের মনে হয়েছিলো কচ্ছপটিকে ধরা একদম অসম্ভব! কিন্তু জেনোর যুক্তি ভুল ছিল। কারণ, একটি নির্দিষ্ট সময়কে অসীম ভাগে বিভক্ত করার পরেও এর যোগফল সেই সময়ের সমানই হবে, যা প্যারাডক্সে আপাতদৃষ্টিতে অসীম মনে হয়।
সুইচ এবং থম্পসনের বাতি
প্যারাডক্স (Paradox) শব্দটির অর্থ ‘চাল’ কিংবা ‘ফাঁকি’। জেনোর চালাকির ফাঁদে পড়ে বহু বিখ্যাত গণিতবিদ দিনের পর দিন অ্যাকিলিস আর কচ্ছপের পেছনে ছুটেছেন। অনেকে সেই কচ্ছপের নিকট পরাজিত হয়েছেন। কিন্তু কেউ কেউ ঠিকই জেনোর চালাকি ধরতে পেরেছেন। কিন্তু জেনো নিজে কখনো সরাসরি উত্তর গ্রহণ করতেন না। তাই কাঁটা দিয়ে কাঁটা তোলার মতো জেনোর প্যারাডক্সের বিরুদ্ধে বেশ কিছু প্যারাডক্স তৈরি করা হয়েছে। এদের মধ্যে সবচেয়ে আলোচিত প্যারাডক্স হচ্ছে ‘থম্পসনের বাতি প্যারাডক্স’।

প্রথমেই আমাদের কল্পনার জগতে একটি বৈদ্যুতিক বাতি এবং একটি সুইচ তৈরি করে নিতে হবে। সুইচ অন করলে বাতি জ্বলে ওঠে এবং অফ করে দিলে তা নিভে যায়। এবার ধরুন, আপনি সুইচ অন করলেন এবং এর ঠিক এক মিনিট পরে সুইচ অফ করে দিলেন। এবার ঠিক ১/২ মিনিট কিংবা ৩০ সেকেণ্ড পর সুইচ পুনরায় অন করে দিলেন। আবার ১/৪ মিনিট কিংবা ১৫ সেকেণ্ড পর সেটা অফ করে দিলেন। এরপর সময়ের হিসাব ঠিক রেখে আবার ১/৮ মিনিট পর সুইচ অন করে দিলেন। অর্থাৎ, প্রতিবার পূর্ব সময়ের অর্ধেক সময়ে সুইচের অবস্থা পরিবর্তন করতে হচ্ছে। এভাবে ঠিক দুই মিনিট পর্যন্ত চালিয়ে যান। এবার আপনাদের নিকট দুটি প্রশ্ন ছুঁড়ে দিলাম।
প্রথম প্রশ্ন: বলুন তো, ঠিক দুই মিনিট পর কি বাতিটি জ্বলবে, নাকি নিভে থাকবে?
দ্বিতীয় প্রশ্ন: যদি শুরুতে সুইচ অন না করে সুইচ অফ করা হয়, তাহলে কি ফলাফল ভিন্ন হবে?

এবার পাঠকরা ভাবতে থাকুন। যে কেউ কাগজে কলমে সেটা হিসাব করে বের করতেও পারেন। মাত্র দু’মিনিটের হিসাব করতে বোধহয় বেশি সময় লাগবে না কারো।
এবার একটি মজার গল্প দিয়ে শেষ করা যাক। ভবিষ্যতে টাইম মেশিনে চড়ে একজন গণিতবিদ প্রাচীনকালের ইলিয়াতিক স্কুলের মাঠে গিয়ে পৌঁছালেন। তখন সেখানে রাত নেমে এসেছে। মেঘমুক্ত আকাশে হাজারো তারকা চকমক করছে। গণিতবিদ চারদিক একপলক দেখে নিয়ে স্কুলঘরের দরজায় টোকা দিলেন। প্রথমদিকে কোনো সাড়া শব্দ নেই। অনেকবার কড়া নাড়ার পর একজন বৃদ্ধ দরজা খুললেন। গণিতবিদ তাকে দেখেই বুঝতে পারলেন, এই লোকটিই জেনো।
জেনো কিন্তু তাকে চিনতে পারলেন না। তিনি খনখনে গলায় জিজ্ঞাসা করলেন, “কী চাই আপনার? এই মধ্যরাতে?” গণিতবিদ একগাল হেসে নিলেন। তারপর হাতের বৈদ্যুতিক বাতিখানা জেনোকে দেখিয়ে বললেন, “থম্পসনের প্যারাডক্সে আপনাকে স্বাগতম, জেনো।” বাকিটা পাঠকরা কল্পনা করে নিন।
ফিচার ইমেজ: Medium